题目内容
(2007
北京宣武模拟)如下图所示，正方体
中，E、F分别是正方形
和ABCD的中心，G是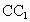
的中点，设GF、
与AB所成的角分别为α、β，则α＋β等于
[
]|
A ．120° |
B ．60° |
C ．75° |
D ．90° |
答案：D
解析：
解析：
练习册系列答案
相关题目
中，E、F分别是正方形和ABCD的中心，G是的中点，设GF、与AB所成的角分别为α、β，则α＋β等于
题目内容
(2007
北京宣武模拟)如下图所示，正方体中，E、F分别是正方形和ABCD的中心，G是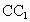的中点，设GF、与AB所成的角分别为α、β，则α＋β等于
[
]|
A ．120° |
B ．60° |
C ．75° |
D ．90° |
分别是双曲线
的左、右焦点，P为双曲线左支上任意一点，若
的最小值为8a，则该双曲线离心率e的取值范围是________．
R)，其中[x]表示不超过x的最大整数．
，f(x)的值域为
，现将
，试求
与
表示等差数列
的前n项和，且
若
，则n=________．
，路段CD发生堵车事件的概率为
．)
