题目内容
对于向量 ,
,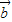 ,
,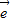 及实数x,y,x1,x2,λ,给出下列四个条件:
及实数x,y,x1,x2,λ,给出下列四个条件:①
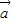 +
+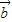 =3
=3 且
且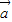 -
- =5
=5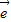 ; ②x1
; ②x1 +x2
+x2 =
=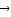
③
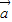 =λ
=λ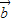 (
(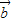 ≠
≠ )且λ唯一; ④x
)且λ唯一; ④x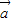 +y
+y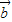 =
=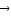 (x+y=0)
(x+y=0)其中能使
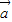 与
与 共线的是( )
共线的是( )A.①②
B.②④
C.①③
D.③④
【答案】分析:由①可得  ,故
,故 与
与  共线,故①满足条件.
共线,故①满足条件.
对于②,当实数x1=x2=0 时, 与
与  为任意向量,故②不满足条件.
为任意向量,故②不满足条件.
由两个向量共线的条件,可得③中的 与
与  共线,故③满足条件.
共线,故③满足条件.
对于④,当x=y=0时,不能推出 与
与  一定共线.
一定共线.
解答:解:对于①,由 ,
, ,解得
,解得  ,
, ,
,
显然 ,故
,故 与
与  共线,故①满足条件.
共线,故①满足条件.
对于②,当实数x1=x2=0 时, 与
与  为任意向量,不能推出
为任意向量,不能推出 与
与  一定共线,故②不满足条件.
一定共线,故②不满足条件.
对于③,∵ ,∴
,∴ 与
与  共线,故③满足条件.
共线,故③满足条件.
对于④,当x=y=0时,不能推出 与
与  一定共线,故②不满足条件.
一定共线,故②不满足条件.
故选C.
点评:本题主要考查平面向量基本定理及其几何意义,两个向量共线的条件,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.
 ,故
,故 与
与  共线,故①满足条件.
共线,故①满足条件.对于②,当实数x1=x2=0 时,
 与
与  为任意向量,故②不满足条件.
为任意向量,故②不满足条件.由两个向量共线的条件,可得③中的
 与
与  共线,故③满足条件.
共线,故③满足条件.对于④,当x=y=0时,不能推出
 与
与  一定共线.
一定共线.解答:解:对于①,由
 ,
, ,解得
,解得  ,
, ,
,显然
 ,故
,故 与
与  共线,故①满足条件.
共线,故①满足条件.对于②,当实数x1=x2=0 时,
 与
与  为任意向量,不能推出
为任意向量,不能推出 与
与  一定共线,故②不满足条件.
一定共线,故②不满足条件.对于③,∵
 ,∴
,∴ 与
与  共线,故③满足条件.
共线,故③满足条件.对于④,当x=y=0时,不能推出
 与
与  一定共线,故②不满足条件.
一定共线,故②不满足条件.故选C.
点评:本题主要考查平面向量基本定理及其几何意义,两个向量共线的条件,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.

练习册系列答案
相关题目
 ,
, ,
, 及实数x,y,x1,x2,λ,给出下列四个条件:
及实数x,y,x1,x2,λ,给出下列四个条件:
 ,
, ,
, 及实数x,y,x1,x2,λ,给出下列四个条件:
及实数x,y,x1,x2,λ,给出下列四个条件: +
+ =3
=3 且
且 -
- =5
=5 ; ②x1
; ②x1 +x2
+x2 =
=
 =λ
=λ (
( ≠
≠ )且λ唯一; ④x
)且λ唯一; ④x +y
+y =
= (x+y=0)
(x+y=0) 与
与 共线的是( )
共线的是( ) ,
, ,
, 及实数x,y,x1,x2,λ,给出下列四个条件:
及实数x,y,x1,x2,λ,给出下列四个条件: +
+ =3
=3 且
且 ﹣
﹣ =5
=5 ;
;  +x2
+x2 =
= ③
③ =λ
=λ (
( ≠
≠ )且λ唯一;
)且λ唯一;  +y
+y =
= (x+y=0)其中能使
(x+y=0)其中能使 与
与 共线的是
共线的是