题目内容
已知数列{an}的前n项和为Sn,且满足Sn=2an﹣1(n∈N+)
(1)求数列{an}的通项公式an;
(2)设bn=![]() ,数列{bn}的前n项和Tn,求证:
,数列{bn}的前n项和Tn,求证:![]() ≤Tn<1.
≤Tn<1.
考点:
数列与不等式的综合;数列的求和;数列递推式.
专题:
综合题.
分析:
(1)根据数列递推式,再写一式,两式相减,即可求得数列的通项;
(2)确定数列的通项,利用叠加法求和,证明是递增数列,即可证得结论.
解答:
(1)解:当n=1时,a1=S1=2a1﹣1,∴a1=1
当n≥2时,an=Sn﹣Sn﹣1=(2an﹣1)﹣(2an﹣1﹣1),∴an=2an﹣1∴数列{an}是首项为a1=1,公比为2的等比数列,
∴数列{an}的通项公式是an=2n﹣1;
(2)证明:bn=![]() =2(
=2(![]() ﹣
﹣![]() )
)
∴Tn=b1+b2+…+bn=2[(![]() ﹣
﹣![]() )+(
)+(![]() ﹣
﹣![]() )+…+(
)+…+(![]() ﹣
﹣![]() )]=2(
)]=2(![]() )<1
)<1
∵Tn+1﹣Tn=bn+1=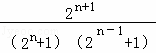 >0
>0
∴数列{Tn}是递增数列
∵T1=![]()
∴![]() ≤Tn<1
≤Tn<1
点评:
本题考查数列的通项,考查数列的求和,考查不等式的证明,解题的关键是确定数列的通项,属于中档题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |