题目内容
若数列{an}满足:a1=1,an+1=2an(n∈N+),则a5= .
【答案】分析:(法一):由an+1=2an,a1=1可得数列{an}是以1为首项,以2为公比的等比数列,由等比数列的通项公式可求an,然后把n=5代入到通项中即可求
(法二):由an+1=2an=22an-1=23an-2=…=2na1=2n可求an,然后把n=5代入到通项中即可求
解答:解:(法一):∵an+1=2an,a1=1
∴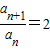
∴数列{an}是以1为首项,以2为公比的等比数列
由等比数列的通项公式可得,an=2n-1
∴a5=24=16
(法二):∵an+1=2an=22an-1=23an-2=…=2na1=2n
∴an=2n-1
a5=24=16
故答案为:16
点评:本题主要考查了利用数列的递推公式求解数列的项,解题的关键是由已知递推公式求解出数列的通项公式,要主要掌握解答本题中用的方法:等比数列的通项公式及迭代的方法
(法二):由an+1=2an=22an-1=23an-2=…=2na1=2n可求an,然后把n=5代入到通项中即可求
解答:解:(法一):∵an+1=2an,a1=1
∴
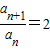
∴数列{an}是以1为首项,以2为公比的等比数列
由等比数列的通项公式可得,an=2n-1
∴a5=24=16
(法二):∵an+1=2an=22an-1=23an-2=…=2na1=2n
∴an=2n-1
a5=24=16
故答案为:16
点评:本题主要考查了利用数列的递推公式求解数列的项,解题的关键是由已知递推公式求解出数列的通项公式,要主要掌握解答本题中用的方法:等比数列的通项公式及迭代的方法

练习册系列答案
相关题目