题目内容
设F1、F2分别是椭圆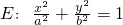 ,(a>b>0)的左、右焦点,P是该椭圆上一个动点,且|PF1|+|PF2|=8,
,(a>b>0)的左、右焦点,P是该椭圆上一个动点,且|PF1|+|PF2|=8, .
.
(1)求椭圆E的方程;
(2)求出以点M(1,1)为中点的弦所在的直线方程.
解:(1)∵椭圆上一个动点P满足|PF1|+|PF2|=8,
∴2a=8,可得a=4
又∵焦距2c= ,∴c=2
,∴c=2 ,可得b2=a2-c2=4
,可得b2=a2-c2=4
因此,椭圆E的方程是: ;
;
(2)根据题意,以M(1,1)为中点的弦所在直线的斜率是存在的
设以点M(1,1)为中点的弦方程为y-1=k(x-1),与椭圆 联解消去y,
联解消去y,
得(1+4k2)x2+8k(1-k)x+4k2-8k-12=0,
设弦的端点坐标为A(x1,y1),B(x2,y2)
由根与系数的关系,得x1+x2=
∵M(1,1)为弦AB的中点,
∴ (x1+x2)=1,可得
(x1+x2)=1,可得 =2,解之得k=-
=2,解之得k=-
因此,以点M(1,1)为中点的弦所在的直线方程为y-1=- (x-1),
(x-1),
化简整理得x+4y-5=0,即为所求直线方程.
分析:(1)根据椭圆的定义,可得2a=|PF1|+|PF2|=8,从而得到a=4.再根据焦距 得到c=
得到c= ,利用平方关系算出b2的值,即可得到椭圆E的方程;
,利用平方关系算出b2的值,即可得到椭圆E的方程;
(2)设以点M(1,1)为中点的弦方程为y-1=k(x-1),与椭圆E方程消去y,得(1+4k2)x2+8k(1-k)x+4k2-8k-12=0,
再由一元二次方程根与系数的关系列式,即可解出斜率k=- ,进而可以得到以点M(1,1)为中点的弦所在的直线方程.
,进而可以得到以点M(1,1)为中点的弦所在的直线方程.
点评:本题给出椭圆E的特征,求椭圆E方程并求以M为中点的弦所在直线方程,着重考查了椭圆的标准方程与简单几何性质、椭圆与直线的位置关系等知识,属于基础题.
∴2a=8,可得a=4
又∵焦距2c=
 ,∴c=2
,∴c=2 ,可得b2=a2-c2=4
,可得b2=a2-c2=4因此,椭圆E的方程是:
 ;
;(2)根据题意,以M(1,1)为中点的弦所在直线的斜率是存在的
设以点M(1,1)为中点的弦方程为y-1=k(x-1),与椭圆
 联解消去y,
联解消去y,得(1+4k2)x2+8k(1-k)x+4k2-8k-12=0,
设弦的端点坐标为A(x1,y1),B(x2,y2)
由根与系数的关系,得x1+x2=

∵M(1,1)为弦AB的中点,
∴
 (x1+x2)=1,可得
(x1+x2)=1,可得 =2,解之得k=-
=2,解之得k=-
因此,以点M(1,1)为中点的弦所在的直线方程为y-1=-
 (x-1),
(x-1),化简整理得x+4y-5=0,即为所求直线方程.
分析:(1)根据椭圆的定义,可得2a=|PF1|+|PF2|=8,从而得到a=4.再根据焦距
 得到c=
得到c= ,利用平方关系算出b2的值,即可得到椭圆E的方程;
,利用平方关系算出b2的值,即可得到椭圆E的方程;(2)设以点M(1,1)为中点的弦方程为y-1=k(x-1),与椭圆E方程消去y,得(1+4k2)x2+8k(1-k)x+4k2-8k-12=0,
再由一元二次方程根与系数的关系列式,即可解出斜率k=-
 ,进而可以得到以点M(1,1)为中点的弦所在的直线方程.
,进而可以得到以点M(1,1)为中点的弦所在的直线方程.点评:本题给出椭圆E的特征,求椭圆E方程并求以M为中点的弦所在直线方程,着重考查了椭圆的标准方程与简单几何性质、椭圆与直线的位置关系等知识,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
设F1、F2分别是椭圆
+
=1(a>b>0)的左、右焦点,P是其右准线上纵坐标为
c(c为半焦距)的点,且|F1F2|=|F2P|,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 设F1、F2分别是椭圆
设F1、F2分别是椭圆