题目内容
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.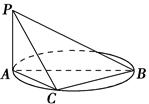
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值..
(1)见解析(2)
解析

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
题目内容
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值..
(1)见解析(2)
解析

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案