题目内容
20.求函数y=$\sqrt{x}$+$\sqrt{3-3x}$的值域.分析 利用换元法,设u=$\sqrt{x}$,v=$\sqrt{3-3x}$,u、v≥0,得出3u2+v2=3;
再设u=cosθ,v=$\sqrt{3}$sinθ,0≤θ≤$\frac{π}{2}$,求函数y=cosθ+$\sqrt{3}$sinθ在θ∈[0,$\frac{π}{2}$]的值域即可.
解答 解:设u=$\sqrt{x}$,v=$\sqrt{3-3x}$,且u、v≥0,
∴3u2+v2=3;
令u=cosθ,v=$\sqrt{3}$sinθ,且0≤θ≤$\frac{π}{2}$,
∴y=cosθ+$\sqrt{3}$sinθ=2sin(θ+$\frac{π}{6}$);
又∵$\frac{π}{6}$≤θ+$\frac{π}{6}$≤$\frac{2π}{3}$,
∴$\frac{1}{2}$≤sin(θ+$\frac{π}{6}$)≤1,
∴1≤2sin(θ+$\frac{π}{6}$)≤2,
即1≤y≤2;
∴函数y=$\sqrt{x}$+$\sqrt{3-3x}$的值域是[1,2].
点评 本题考查了求函数值域的应用问题,解题时应利用换元法,把问题转化为求三角函数在闭区间上的最值问题,是综合性题目.

练习册系列答案
相关题目
11.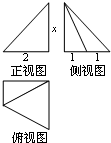 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
5.已知${∫}_{0}^{t}$xdx=2,则${∫}_{-t}^{0}$xdx等于( )
| A. | 0 | B. | 2 | C. | -1 | D. | -2 |
10.已知椭圆的焦点在x轴上,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$,直线l:y=-2,任取椭圆上一点P(异于短轴端点M,N)直线MP,NP分别交直线l于点T,S,则|ST|的最小值是( )
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8$\sqrt{2}$ |
 如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.