题目内容

直线l过抛物线y2=x的焦点F,交抛物线于A、B两点,且点A在x轴上方,若直线l的倾斜角θ≥,则|FA|的取值范围是

A.［,)          B.(,+］        C.(,］            D.(,1+］

D

解析:由题意作图,作抛物线y2=x的准线l,过点A作AA1⊥l于点A1,过A作AC⊥x轴,则A点坐标为(|FA|cosθ+,|FA|sinθ).

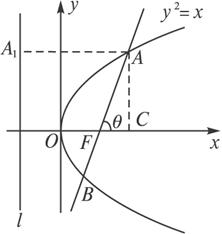
由抛物线的定义可知|AA1|=|FA|,∴当θ=时,|AA1|=|FA|=|FA|·cos++.

∴|FA|=1+.又≤θ＜π,∴＜|FA|≤1+.

练习册系列答案
相关题目
设斜率为2的直线l过抛物线y2=ax（a≠0）的焦点F，且和y轴交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（　　）
A、y2=±4xB、y2=4xC、y2=±8xD、y2=8x
已知斜率为2的直线l过抛物线y2=ax的焦点F，且与y轴相交于点A，若△OAF（O为坐标原点）的面积为4，则抛物线方程为（　　）
A、y2=4xB、y2=8xC、y2=4x或y2=-4xD、y2=8x或y2=-8x
设斜率为k的直线l过抛物线y2=8x的焦点F，且和y轴交于点A，若△OAF （O为坐标原点）的面积为4，则实数k的值为（　　）
A、±2B、±4C、2D、4
在平面直角坐标系xOy中，直线l过抛物线y2=4x的焦点F交抛物线于A、B两点．
（1）若|AB|=8，求直线l的斜率
（2）若|AF|=m，|BF|=n．求证
1
m
+
1
n
为定值．
（1）直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线相交于A（x1，y1），B（x2，y2）两点，证明：y1y2=-p2；
（2）直线l过抛物线y2=2px（p＞0）的焦点，且与抛物线相交于A（x1，y1），B（x2，y2）两点，点C在抛物线的准线上，且BC∥x轴，证明：直线AC经过原点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网