题目内容
已知f(x)=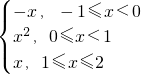
(1)求f( ),f[f(-
),f[f(- )]值;
)]值;
(2)若f(x)= ,求x值;
,求x值;
(3)作出该函数简图;
(4)求函数值域.
 解:(1)由题意得:
解:(1)由题意得:f(
 )=
)= ,
,又f(-
 )=
)=
∴f[f(-
 )]=f(
)]=f( )=
)= ;
;(2)当-1≤x<0时,f(x)=-x=
 ?x=-
?x=- 符合题意
符合题意当0≤x<1时,f(x)=x2=
 ?x=
?x= 或x=-
或x=- (不合,舍去)
(不合,舍去)当1≤x≤2时,f(x)=x=
 (不合题意,舍去)
(不合题意,舍去)综上:x=-
 或
或 .
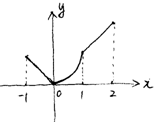
.(3)其简图如下图所示:
(4)由(3)中函数的简图可得
函数值y的最大值为2,最小值为0,
故y∈[0,2],
即函数值域为:[0,2].
分析:(1)先求f(
 ),f(-
),f(- ),再判断f(
),再判断f( )与1和2的大小,求解f[f(-
)与1和2的大小,求解f[f(- )]值;
)]值;(2)根据题意,对x的进行分类讨论:当-1≤x<0时;当0≤x<1时;当1≤x≤2时.结合f(x)的函数值等于
 求出x即可;
求出x即可;(3)函数f(x)=
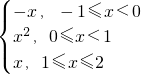 ,分三段作出其图象;
,分三段作出其图象;(4)根据(3)中函数简图,数形结合可分析出函数f(x)的值域即可.
点评:本题考查分段函数求值问题,考查一次函数、二次函数图象的变化及分段函数图象的作法.属基本题型、基本运算的考查.

练习册系列答案
相关题目
已知f(x)=a-
是定义在R上的奇函数,则f-1(-
)的值是( )
| 2 |
| 2x+1 |
| 3 |
| 5 |
A、
| ||
| B、-2 | ||
C、
| ||
D、
|