题目内容
随机抽取50名男生测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],其中第六组的频数为4,第八组的频率为0.04,现从这两组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,则满足:|x-y|≤5的事件概率为
【答案】分析:首先根据频率分布表,做出两组的频数,即试验发生包含的人数,后面的问题转化成等可能事件的概率,试验发生包含的事件数是15,满足条件的事件数是7,根据等可能事件的概率得到结果.
解答:解:第四组是[170,175),它的频数是4,
第六组是[180,185),它的频率是0.04,频数是0.04×50=2,
两组一共有6个人,从中随机的抽取两个人,共有C62=15种结果,
满足条件|x-y|≤5的事件,包括从第四组取两个,有一种结果,
从第六组取两个有C42=6种结果,
满足条件共有1+6=7种结果,
根据等可能事件的概率公式得到P= ,
,
故答案为 .
.
点评:本题考查频率分布表,考查等可能事件的概率,是一个综合题,解题的关键是在等可能事件中看出满足条件的事件数.
解答:解:第四组是[170,175),它的频数是4,
第六组是[180,185),它的频率是0.04,频数是0.04×50=2,
两组一共有6个人,从中随机的抽取两个人,共有C62=15种结果,
满足条件|x-y|≤5的事件,包括从第四组取两个,有一种结果,
从第六组取两个有C42=6种结果,
满足条件共有1+6=7种结果,
根据等可能事件的概率公式得到P=
 ,
,故答案为
 .
.点评:本题考查频率分布表,考查等可能事件的概率,是一个综合题,解题的关键是在等可能事件中看出满足条件的事件数.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 (2013•青岛一模)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
(2013•青岛一模)从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.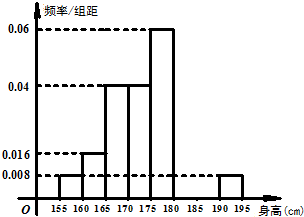 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人. 从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.