题目内容
如图，直三棱柱ABC-A1B1C1中，AC=BC=CC1=1，且AC⊥BC，过C1作截面分别交AC，BC于E，F，且二面角C1-EF-C为60°，则三棱锥C1-EFC体积的最小值为（ ）
A．
B．
C．
D．
【答案】分析：先根据二面角求出在三角形CEF斜边EF边上的高，设CE=a，CF=b，则EF=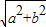
，然后等面积建立等式，再利用基本不等式求出ab的最值，利用体积公式表示出三棱锥C1-EFC体积，从而求出体积的最小值．
解答：解：∵二面角C1-EF-C为60°
∴在三角形CEF斜边EF边上的高为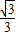
设CE=a，CF=b，则EF=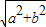
在三角形CEF中ab=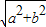
•
≥
∴
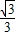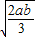
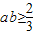
三棱锥C1-EFC体积V=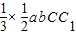
=
≥
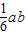故选B．
点评：本题主要考查了二面角的应用，以及锥体的体积和基本不等式求最值，属于中档题．
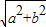，然后等面积建立等式，再利用基本不等式求出ab的最值，利用体积公式表示出三棱锥C1-EFC体积，从而求出体积的最小值．解答：解：∵二面角C1-EF-C为60°
∴在三角形CEF斜边EF边上的高为
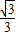
设CE=a，CF=b，则EF=
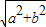
在三角形CEF中ab=
•≥∴
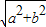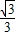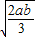
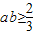
三棱锥C1-EFC体积V=
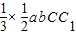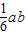=≥故选B．
点评：本题主要考查了二面角的应用，以及锥体的体积和基本不等式求最值，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，直三棱柱ABC-A1B1C1中，
如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．