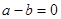题目内容
不等边△ABC的三个内角A,B,C所对的边分别是a,b,c,且lgsinA,lgsinB,lgsinC成等差数列,则直线xsin2A+ysinA=a与直线xsin2B+ysinC=c的位置关系是
| A.平行 | B.垂直 | C.重合 | D.相交但不垂直 |
C
解:∵lgsinA,lgsinB,lgsinC成等差数列,
∴sin2B=sinA?sinC,
∴直线xsin2A+ysinA=a与直线xsin2B+ysinC=c的x的系数之比
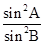 =
=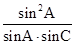 =
=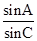 ,
,
y的系数只比为: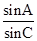 ,
,
两直线的常数项之比为: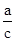 ,
,
又△ABC的三个内角A,B,C所对的边分别是a,b,c,由正弦定理得:
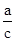 =
=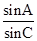 ,
,
∴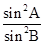 =
=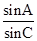 =
=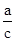 .
.
故选C.
∴sin2B=sinA?sinC,
∴直线xsin2A+ysinA=a与直线xsin2B+ysinC=c的x的系数之比
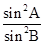 =
=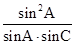 =
=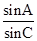 ,
,y的系数只比为:
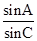 ,
,两直线的常数项之比为:
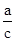 ,
,又△ABC的三个内角A,B,C所对的边分别是a,b,c,由正弦定理得:
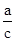 =
=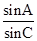 ,
,∴
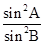 =
=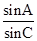 =
=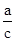 .
.故选C.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 经过点
经过点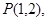 且与两点
且与两点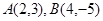 的距离相等,则直线
的距离相等,则直线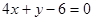 或
或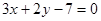
 或
或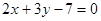
 不经过第一象限,且
不经过第一象限,且 ,则直线
,则直线 的倾斜角的取值范围是( )
的倾斜角的取值范围是( ) 



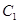 :
: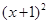 +
+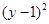 =1,圆
=1,圆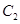 与圆
与圆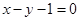 对称,则圆
对称,则圆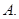
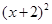 +
+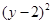 =1
=1 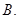
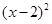 +
+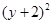 =1
=1 
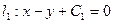 ,
,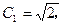
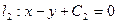 ,
,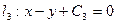 ,……,
,……,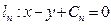 (其中
(其中 ),当
),当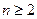 时,直线
时,直线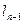 与
与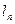 间的距离为n.
间的距离为n.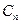 ;
;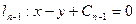 与直线
与直线 及x轴、y轴围成图形的面积.
及x轴、y轴围成图形的面积. 且在两坐标轴上的截距相等,则这直线方程为( )
且在两坐标轴上的截距相等,则这直线方程为( )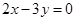
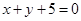
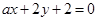 与直线
与直线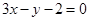 垂直,那么系数
垂直,那么系数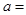 ( )
( )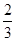
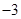
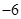
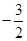
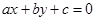 的倾斜角为
的倾斜角为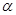 ,且
,且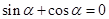 ,则
,则 满足( )
满足( )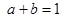 B
B 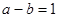 C
C 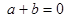 D
D