题目内容
若两条曲线的极坐标方程分别为p=l与p=2cos(θ+| π | 3 |
分析:先将原极坐标方程中的三角函数式利用和角公式化开后,两边同乘以ρ后化成直角坐标方程,再利用直角坐标方程进行判断.
解答:解:由ρ=1得x2+y2=1,(2分)
又∵ρ=2cos(θ+
)=cosθ-
sinθ,∴ρ2=ρcosθ-
ρsinθ
∴x2+y2-x+
y=0,(4分)
由
得A(1,0),B(-
,-
),(8分)
∴AB=
=
.(10分)
又∵ρ=2cos(θ+
| π |
| 3 |
| 3 |
| 3 |
∴x2+y2-x+
| 3 |
由
|
| 1 |
| 2 |
| ||
| 2 |
∴AB=
(1+
|
| 3 |
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
相关题目
 (2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤.
(2011•江苏二模)选答题:本大题共四小题,请从这4题中选作2小题,如果多做,则按所做的前两题记分.每小题10分,共20分,解答时应写出文字说明,证明过程或演算步骤. ]的变换作用下的曲线方程.
]的变换作用下的曲线方程. cos2θ+
cos2θ+ sin2θ<
sin2θ< .
.
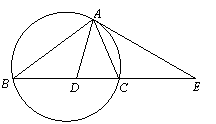 ∠BAC的平分线与BC交于点D.
∠BAC的平分线与BC交于点D.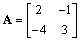 ,
,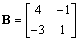 ,求满足
,求满足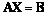 的二阶矩阵
的二阶矩阵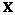 .
.