题目内容
已知直线 过点
过点 ,圆
,圆 :
: .
.
(1)求截得圆 弦长最长时
弦长最长时 的直线方程;
的直线方程;
(2)若直线 被圆N所截得的弦长为
被圆N所截得的弦长为 ,求直线
,求直线 的方程.
的方程.
【答案】
解:(1)显然,当直线 通过圆心N时,被截得的弦长最长.………2分
通过圆心N时,被截得的弦长最长.………2分
由 ,得
,得 
故所求直线 的方程为
的方程为 
即  ………4分
………4分
 (2)设直线
(2)设直线 与圆N交于
与圆N交于 两点(如右图)
两点(如右图)
作 交直线
交直线 于点D,显然D为AB的中点.且有
于点D,显然D为AB的中点.且有
 ………6分
………6分
(Ⅰ)若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 
将 代入
代入 ,得
,得
 [来源:Zxxk.Com]
[来源:Zxxk.Com]
解,得  ,
,
因此  符合题意………8分
符合题意………8分
(Ⅱ)若直线 的斜率存在,不妨设直线
的斜率存在,不妨设直线 的方程为
的方程为  即:
即:
由 ,得
,得  ,
,
因此  ………10分
………10分
又因为点N到直线 的距离
的距离
所以  即:
即:
此时 直线 的方程为
的方程为 
综上可知,直线 的方程为
的方程为  或
或 ………12分
………12分
【解析】

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
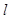 过点
过点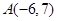 与圆
与圆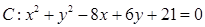 相切,
相切, 过点
过点 与圆
与圆 相切,
相切,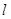 过点
过点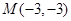 ,圆N:
,圆N: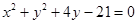 ,
,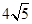 .
.