题目内容
已知实数a＞0，且a≠1，函数f（x）=loga|x|在（-∞，0）上是减函数，函数g(x)=ax+
，则下列选项正确的是（ ）
| 1 | ||
|
| A．g（-3）＜g（2）＜g（4） | B．g（-3）＜g（4）＜g（2） | C．g（4）＜g（-3）＜g（2） | D．g（2）＜g（-3）＜g（4） |
∵实数a＞0，且a≠1，函数f（x）=loga|x|在（-∞，0）上是减函数，
∴令u=|x|，则y=logau，
由u=|x|在（-∞，0）上是减函数，及复合函数同增异减的原则，可得外函数y=logau为增函数，即a＞1
∵函数g(x)=ax+
为偶函数且函数在[0，+∞）上单调递增，在（-∞，0]上单调递减
∵|2|＜|-3|＜|4|
∴g（2）＜g（-3）＜g（4）
故选D．
∴令u=|x|，则y=logau，
由u=|x|在（-∞，0）上是减函数，及复合函数同增异减的原则，可得外函数y=logau为增函数，即a＞1
∵函数g(x)=ax+
| 1 | ||
|
∵|2|＜|-3|＜|4|
∴g（2）＜g（-3）＜g（4）
故选D．
练习册系列答案
相关题目
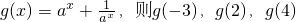的大小关系为______．
，则下列选项正确的是（ ）