题目内容

随机变量ξ的分布列如右表所示，则Eξ=
0.24
0.24
；
ξ -1 0 1
P m2 1-1.4m 0.4
分析：先根据离散型随机变量所有取值的概率和为1，可求m的值，进而可求期望．
解答：解：由题意知，m2+1-1.4m+0.4=1，
∴m=0.4
∴Eξ=-0.16+0.4=0.24
故答案为0.24．
点评：本题以分布列为载体，考查概率的性质，考查数学期望，属于基础题．
练习册系列答案
相关题目
已知离散型随机变量X的分布列如表．若EX=0，DX=1，则a=
 
，b=
 
．
X -1 0 1 2
P a b c
1
12
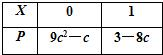精英家教网若离散型随机变量X的分布列如图，则常数c的值为（　　）
A、
2
3
或
1
3
B、
2
3
C、
1
3
D、1
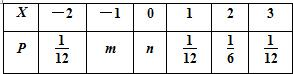精英家教网已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=
1
6
，则m，n的值分别为（　　）
A、
1
12
，
1
2
B、
1
6
，
1
6
C、
1
4
，
1
3
D、
1
3
，
1
4
已知离散型随机变量X 的分布列如右图．若E（X）=0，D（X）=1，则a、b、c的值依次为
5
12
，
1
4
，
1
4
5
12
，
1
4
，
1
4
．
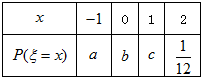精英家教网已知离散型随机变量x的分布列如右表．若Eξ=0，Dξ=1，则符合条件的一组数（a，b，c）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网