题目内容
已知f(x)是单调递增的一次函数,f(f(x))=4x+3,则f(x)的解析式为
f(x)=2x+1
f(x)=2x+1
.分析:利用待定系数法设f(x)=kx+b,k>0,然后利用条件f(f(x))=4x+3,求解即可.
解答:解:∵f(x)是单调递增的一次函数,
∴f(x)=kx+b,k>0,
由f(f(x))=4x+3,
得f(kx+b)=k(kx+b)+b=4x+3
即k2x+kb+b=4x+3,
∴
,解得k=2,b=1,
∴f(x)=kx+b=2x+1.
故答案为:f(x)=2x+1.
∴f(x)=kx+b,k>0,
由f(f(x))=4x+3,
得f(kx+b)=k(kx+b)+b=4x+3
即k2x+kb+b=4x+3,
∴
|
∴f(x)=kx+b=2x+1.
故答案为:f(x)=2x+1.
点评:本题主要考查利用待定系数法求一次函数的方程问题,比较基础.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
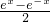 ,则它是 ________函数(填“奇”或者“偶”),在R上单调递 ________
,则它是 ________函数(填“奇”或者“偶”),在R上单调递 ________