题目内容
函数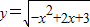
的单调递减区间是（ ）A．（-∞，1）
B．（1，+∞）
C．[-1，1]
D．[1，3]
【答案】分析：先确定函数的定义域，再考虑二次函数的单调性，即可求得结论．
解答：解：令t=-x2+2x+3，则由-x2+2x+3≥0可得-1≤x≤3
∵-x2+2x+3=-（x-1）2+4，∴当1≤x≤3时，函数单调递减
∵
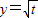在定义域内为增函数
∴函数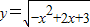
的单调递减区间是[1，3]．
故选D．
点评：本题考查函数的单调性，解题的关键是确定函数的定义域，确定二次函数的单调性，属于中档题．
解答：解：令t=-x2+2x+3，则由-x2+2x+3≥0可得-1≤x≤3
∵-x2+2x+3=-（x-1）2+4，∴当1≤x≤3时，函数单调递减
∵
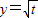在定义域内为增函数∴函数
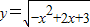的单调递减区间是[1，3]．故选D．
点评：本题考查函数的单调性，解题的关键是确定函数的定义域，确定二次函数的单调性，属于中档题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
的单调递减区间是 . 
的单调递减区间是 . (科网