题目内容
求和Sn=x+2x2+3x3+…+nxn.
思路分析：由于{n}是等差数列，而当x≠0时，{xn}是等比数列，故可采用错位相减法.
解：当x=0,Sn=0;当x=1时，S1=
;
当x≠1且x≠0时，∵Sn=x+2x2+3x3+…+nxn, ①
∴xSn=x2+2x3+3x4+…+(n-1)xn+nxn+1. ②
①-②，得(1-x)Sn=x+x2+x3+…+xn-nxn+1=x
-nxn+1.
∴Sn=
·［nxn+1-(n+1)xn+1］.
∴Sn=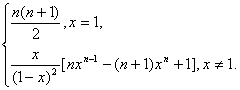
练习册系列答案
相关题目