题目内容
在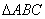 中,角
中,角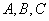 的对边分别为
的对边分别为 ,若
,若 .
.
(Ⅰ)求证: 、
、 、
、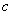 成等差数列;
成等差数列;
(Ⅱ)若 ,求
,求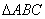 的面积.
的面积.
(1)根据已知的边角关系,结合二倍角公式来化简得到证明。
(2)
解析试题分析:(1)证明:
即
由正弦定理得:
即

由正弦定理:
整理得: ,故
,故 成等差数列
成等差数列
(2)由 及余弦定理得:
及余弦定理得:
∴
又由(1)知 ,可得
,可得
∴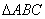 的面积
的面积
考点:解三角形,等差数列
点评:主要是考查了正弦定理和余弦定理以及等差数列的综合运用 ,属于中档题。

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 内的空地上植造“绿地
内的空地上植造“绿地 ”,其中
”,其中 ,
, 长可根据需要进行调节(
长可根据需要进行调节(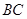 足够长),现规划在
足够长),现规划在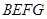 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积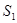 与种花的面积
与种花的面积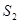 的比
的比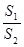 为
为 ,
,
 ,将
,将 的函数关系;
的函数关系; 为多长时,
为多长时, 分别为
分别为 三个内角
三个内角 的对边,
的对边,
 ;
;  ,
, ;求
;求 。
。 ,
, ,B=45°求A、C及c
,B=45°求A、C及c  所对的边分别是
所对的边分别是 ,且
,且 。
。 的值;
的值; ,
, 的面积
的面积 ,求
,求 的值。
的值。 中,
中, 分别是角
分别是角 的对边,
的对边, ,
, .
. 的值;
的值; ,求边
,求边 的长.
的长. 中,内角
中,内角 所对的分别是
所对的分别是 ,已知
,已知 ;
; 和
和 的值; (II)求
的值; (II)求 的值.
的值. ,
, ,求b.
,求b. ;
; 的值.
的值.