题目内容
若斜率为 的直线l与椭圆
的直线l与椭圆 +
+ =1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为 ________.
=1(a>b>0)有两个不同的交点,且这两个交点在x轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为 ________.

分析:根据题意可知:两交点的横坐标为-c,c,纵坐标分别为-
 ,
, ,所以由斜率公式可得:
,所以由斜率公式可得: =
= 转化为:2b2=ac=2(a2-c2),两边同除以a2,转化为了2e2+
转化为:2b2=ac=2(a2-c2),两边同除以a2,转化为了2e2+ e-2=0求解.
e-2=0求解.解答:由题意知:两交点的横坐标为-c,c,纵坐标分别为-
 ,
, ,
,∴由
 =
=
转化为:2b2=ac=2(a2-c2),
即2e2+
 e-2=0,
e-2=0,解得e=
 (负根舍去).
(负根舍去).故答案为:

点评:本题主要考查椭圆的几何性质及直线的斜率公式和离心率公式,同时,还考查了转化思想.

练习册系列答案
相关题目
 ,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点.
,斜率为1的直L与椭C交于A(x1,y1)B(x2,y2)两点. ,直线l过点M(b,0),且
,直线l过点M(b,0),且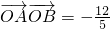 ,求椭圆C的方程;
,求椭圆C的方程; =λ(
=λ( +
+ )(λ>0),若点P在椭C上,λ的取值范围.
)(λ>0),若点P在椭C上,λ的取值范围.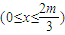 和椭圆弧
和椭圆弧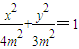

 和椭圆弧
和椭圆弧
