题目内容
设x1<x2,定义区间[x1,x2]的长度为x2-x1.若函数y=2|x|,x∈[a,b]的值域与 的值域相同,则区间[a,b]的长度的最大值与最小值的差为________.
的值域相同,则区间[a,b]的长度的最大值与最小值的差为________.
1
分析:先利用导数正确求出函数 的值域,进而利用单调性求出函数y=2|x|取何定义域时的值域与之相同即可.
的值域,进而利用单调性求出函数y=2|x|取何定义域时的值域与之相同即可.
解答:对于函数 ,∵x≥0,1-x≥0,∴0≤x≤1.∴此函数的定义域为[0,1].
,∵x≥0,1-x≥0,∴0≤x≤1.∴此函数的定义域为[0,1].
 =
= ,令y′=0,解得
,令y′=0,解得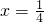 .
.
当 时,y′>0;当
时,y′>0;当 时,y′<0.
时,y′<0.
∴函数f(x)= 在区间
在区间 上单调递增,在区间
上单调递增,在区间 是单调递减.
是单调递减.
又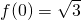 ,f(1)=1,
,f(1)=1, ,∴f(x)max=2,f(x)min=1,
,∴f(x)max=2,f(x)min=1,
函数 的值域为[1,2].
的值域为[1,2].
当x∈[0,1]时,函数y=2|x|,x∈[0,1]的值域为[1,2].
则区间[0,1]的长度的最大值与最小值的差为1.
故答案为1.
点评:正确求出函数 的值域及与利用单调性求出函数y=2|x|取何定义域时的值域相同是解题的关键.
的值域及与利用单调性求出函数y=2|x|取何定义域时的值域相同是解题的关键.
分析:先利用导数正确求出函数
 的值域,进而利用单调性求出函数y=2|x|取何定义域时的值域与之相同即可.
的值域,进而利用单调性求出函数y=2|x|取何定义域时的值域与之相同即可.解答:对于函数
 ,∵x≥0,1-x≥0,∴0≤x≤1.∴此函数的定义域为[0,1].
,∵x≥0,1-x≥0,∴0≤x≤1.∴此函数的定义域为[0,1]. =
= ,令y′=0,解得
,令y′=0,解得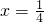 .
.当
 时,y′>0;当
时,y′>0;当 时,y′<0.
时,y′<0.∴函数f(x)=
 在区间
在区间 上单调递增,在区间
上单调递增,在区间 是单调递减.
是单调递减.又
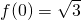 ,f(1)=1,
,f(1)=1, ,∴f(x)max=2,f(x)min=1,
,∴f(x)max=2,f(x)min=1,函数
 的值域为[1,2].
的值域为[1,2].当x∈[0,1]时,函数y=2|x|,x∈[0,1]的值域为[1,2].
则区间[0,1]的长度的最大值与最小值的差为1.
故答案为1.
点评:正确求出函数
 的值域及与利用单调性求出函数y=2|x|取何定义域时的值域相同是解题的关键.
的值域及与利用单调性求出函数y=2|x|取何定义域时的值域相同是解题的关键. 
练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目