题目内容
求函数 的最大值和最小值.
的最大值和最小值.
解:∵ ,
,
∴y=3-2x-x2=4-(x+1)2.
当x=-1时,ymax=4;
当x= 时,
时, .
.
∴函数 的最大值是4,最小值是
的最大值是4,最小值是 .
.
分析:先配方得到y=3-2x-x2=4-(x+1)2.再由x的取值范围确定函数的最大值和最小值.
点评:本题考查函数的最大值和最小值,解题时要认真审题,仔细求解.
 ,
,∴y=3-2x-x2=4-(x+1)2.
当x=-1时,ymax=4;
当x=
 时,
时, .
.∴函数
 的最大值是4,最小值是
的最大值是4,最小值是 .
.分析:先配方得到y=3-2x-x2=4-(x+1)2.再由x的取值范围确定函数的最大值和最小值.
点评:本题考查函数的最大值和最小值,解题时要认真审题,仔细求解.

练习册系列答案
相关题目


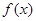 的最大值和最小正周期;
的最大值和最小正周期; 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的向量
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的向量