题目内容
在△ABC中,cosA•cosB+cosA•sinB+sinAcosB+sinA•sinB=2,则△ABC是
- A.等边三角形
- B.等腰非等边的锐角三角形
- C.非等腰的直角三角形
- D.等腰直角三角形
D
分析:逆用两角和的正弦与两角差的余弦公式,再利用正弦函数与余弦函数的有界性即可判断△ABC的形状.
解答:∵cosA•cosB+sinA•sinB=cos(A-B),
cosA•sinB+sinAcosB=sin(A+B),
∴在△ABC中,cosA•cosB+cosA•sinB+sinAcosB+sinA•sinB=2?cos(A-B)+sin(A+B)=2,①
又-1≤cos(A-B)≤1,
-1≤sin(A+B)≤1,
∴-2≤cos(A-B)+sin(A+B)≤2,
由①知,cos(A-B)=1且sin(A+B)=1.
∴A=B= .
.
故△ABC是等腰直角三角形.
故选D.
点评:本题考查三角形的形状判断,逆用两角和的正弦与两角差的余弦公式是关键,考查分析转化能力,属于中档题.
分析:逆用两角和的正弦与两角差的余弦公式,再利用正弦函数与余弦函数的有界性即可判断△ABC的形状.
解答:∵cosA•cosB+sinA•sinB=cos(A-B),
cosA•sinB+sinAcosB=sin(A+B),
∴在△ABC中,cosA•cosB+cosA•sinB+sinAcosB+sinA•sinB=2?cos(A-B)+sin(A+B)=2,①
又-1≤cos(A-B)≤1,
-1≤sin(A+B)≤1,
∴-2≤cos(A-B)+sin(A+B)≤2,
由①知,cos(A-B)=1且sin(A+B)=1.
∴A=B=
 .
.故△ABC是等腰直角三角形.
故选D.
点评:本题考查三角形的形状判断,逆用两角和的正弦与两角差的余弦公式是关键,考查分析转化能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
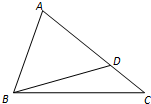 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=