题目内容
已知双曲线C的渐近线方程为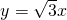 ,右焦点F(c,0)到渐近线的距离为
,右焦点F(c,0)到渐近线的距离为 .
.
(1)求双曲线C的方程;
(2)过F作斜率为k的直线l交双曲线于A、B两点,线段AB的中垂线交x轴于D,求证: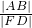 为定值.
为定值.
解:(1)设双曲线方程为3x2-y2=λ(λ>0)…(2分)
由题知c=2,∴ ,∴λ=3…(4分)
,∴λ=3…(4分)
∴双曲线方程为: …(5分)
…(5分)
(2)设直线l的方程为y=k(x-2)代入
整理得(3-k2)x2+4k2x-4k2-3=0…(6分)
设A(x1,y1),B(x2,y2),AB的中点P(x0,y0)
则 ,代入l得:
,代入l得: …(7分)
…(7分)
 …(8分)
…(8分)
AB的垂直平分线方程为 …(9分)
…(9分)
令y=0得 …(10分)
…(10分)
∴ …(11分)
…(11分)
∴ 为定值.…(12分)
为定值.…(12分)
分析:(1)由渐近线方程为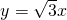 ,可设双曲线方程为3x2-y2=λ(λ>0),由题知c=2,代入可求双曲线方程
,可设双曲线方程为3x2-y2=λ(λ>0),由题知c=2,代入可求双曲线方程
(2)设直线l的方程为y=k(x-2)代入 ,整理得(3-k2)x2+4k2x-4k2-3=0
,整理得(3-k2)x2+4k2x-4k2-3=0
设A(x1,y1),B(x2,y2),AB的中点P(x0,y0)则利用方程的根与系数的关系可求x0,y0.利用弦长公式可表示AB,然后由AB的垂直平分线方程可求D的坐标,进而求出FD,从而可求
点评:本题主要考查了由双曲线的性质求解双曲线的方程,直线与曲线相交求解弦长,解题中要善于应用两直线垂直得斜率之间的关系.
由题知c=2,∴
 ,∴λ=3…(4分)
,∴λ=3…(4分)∴双曲线方程为:
 …(5分)
…(5分)(2)设直线l的方程为y=k(x-2)代入

整理得(3-k2)x2+4k2x-4k2-3=0…(6分)
设A(x1,y1),B(x2,y2),AB的中点P(x0,y0)
则
 ,代入l得:
,代入l得: …(7分)
…(7分) …(8分)
…(8分)AB的垂直平分线方程为
 …(9分)
…(9分)令y=0得
 …(10分)
…(10分)∴
 …(11分)
…(11分)∴
 为定值.…(12分)
为定值.…(12分)分析:(1)由渐近线方程为
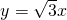 ,可设双曲线方程为3x2-y2=λ(λ>0),由题知c=2,代入可求双曲线方程
,可设双曲线方程为3x2-y2=λ(λ>0),由题知c=2,代入可求双曲线方程(2)设直线l的方程为y=k(x-2)代入
 ,整理得(3-k2)x2+4k2x-4k2-3=0
,整理得(3-k2)x2+4k2x-4k2-3=0设A(x1,y1),B(x2,y2),AB的中点P(x0,y0)则利用方程的根与系数的关系可求x0,y0.利用弦长公式可表示AB,然后由AB的垂直平分线方程可求D的坐标,进而求出FD,从而可求
点评:本题主要考查了由双曲线的性质求解双曲线的方程,直线与曲线相交求解弦长,解题中要善于应用两直线垂直得斜率之间的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目