题目内容
(本小题满分12分)设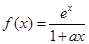 ,其中
,其中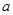 为正实数
为正实数
(1)当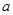
 时,求
时,求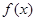 的极值点;
的极值点;
(2)若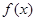 为
为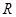 上的单调函数,求
上的单调函数,求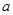 的取值范围。[来源:ZXXK]
的取值范围。[来源:ZXXK]
【答案】
对 求导得
求导得
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
(1)当 时,若
时,若 ,则
,则 ,解得
,解得 ,结合①,可得
,结合①,可得
所以, 是极小值点,
是极小值点, 是极大值点.
是极大值点.
(2)若 为R上的单调函数,则
为R上的单调函数,则 在R上不变号,结合①与条件
在R上不变号,结合①与条件 ,知在R上恒成立,因此
,知在R上恒成立,因此 ,由此并结合
,由此并结合 ,知
,知 .
.
【解析】略

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目






