题目内容
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,
, ,
,
求使 恒成立的实数
恒成立的实数 的取值范围.
的取值范围.
解:(I)由 可得
可得 ,∵
,∵ , ∴
, ∴ ,
,
∴ ,即
,即 ,
,
∴数列 是以
是以 为首项,公比为
为首项,公比为 的等比数列,∴
的等比数列,∴ .
.
(Ⅱ)
∴
由 对任意
对任意 恒成立,即实数
恒成立,即实数 恒成立;
恒成立;
设 ,
, ,
,
∴当 时,数列
时,数列 单调递减,
单调递减, 时,数列
时,数列 单调递增;
单调递增;
又 ,∴数列
,∴数列 最大项的值为
最大项的值为
∴

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
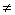 0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{ bn}的前3项。 ,对任意
,对任意 都有
都有 ,且
,且 是增函数,则
是增函数,则
 为抛物线
为抛物线 的焦点,
的焦点, 为该抛物线上三点,若
为该抛物线上三点,若 ,
, 的值为
的值为 B.
B. C.
C. D.12
D.12 中,以原点
中,以原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.若点
轴的正半轴为极轴建立极坐标系.若点 为
为 上一点,点
上一点,点 为曲线
为曲线 为参数)上一点,则
为参数)上一点,则 的最小值为 .
的最小值为 .  的定义域是
的定义域是 B.
B.  C.
C. D.
D. 
 的两条渐近线与直线
的两条渐近线与直线 分别交于
分别交于 两点,
两点, 为该双曲线的右焦点.若
为该双曲线的右焦点.若 , 则该双曲线的离心率的取值范围是
, 则该双曲线的离心率的取值范围是 B.
B. C.
C. D.
D.
 上的一点向圆
上的一点向圆 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( ) C.
C. D.3
D.3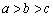 (B)
(B)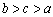 (C)
(C) (D)
(D)