题目内容
正实数数列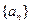 中,
中,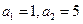 ,且
,且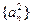 成等差数列.
成等差数列.
(1) 证明数列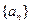 中有无穷多项为无理数;
中有无穷多项为无理数;
(2)当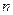 为何值时,
为何值时,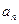 为整数,并求出使
为整数,并求出使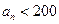 的所有整数项的和.
的所有整数项的和.
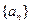 中,
中,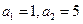 ,且
,且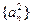 成等差数列.
成等差数列.(1) 证明数列
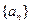 中有无穷多项为无理数;
中有无穷多项为无理数;(2)当
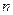 为何值时,
为何值时,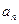 为整数,并求出使
为整数,并求出使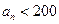 的所有整数项的和.
的所有整数项的和. (
(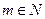 )时,
)时,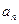 为整数;
为整数;考查等差数列及数列分组求和知识
证明:(1)由已知有: ,从而
,从而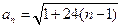 ,
,
方法一:取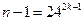 ,则
,则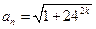 (
(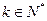 )
)
用反证法证明这些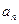 都是无理数.
都是无理数.
假设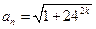 为有理数,则
为有理数,则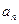 必为正整数,且
必为正整数,且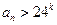 ,
,
故 .
.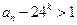 ,与
,与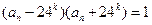 矛盾,
矛盾,
所以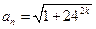 (
(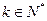 )都是无理数,即数列
)都是无理数,即数列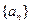 中有无穷多项为无理数;
中有无穷多项为无理数;
方法二:因为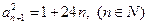 ,当
,当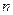 的末位数字是
的末位数字是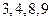 时,
时,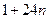 的末位数字是
的末位数字是 和
和 ,它不是整数的平方,也不是既约分数的平方,故此时
,它不是整数的平方,也不是既约分数的平方,故此时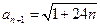 不是有理数,因这种
不是有理数,因这种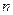 有无穷多,故这种无理项
有无穷多,故这种无理项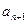 也有无穷多.
也有无穷多.
(2) 要使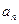 为整数,由
为整数,由 可知:
可知:
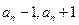 同为偶数,且其中一个必为3的倍数,所以有
同为偶数,且其中一个必为3的倍数,所以有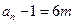 或
或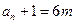
当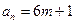 时,有
时,有 (
(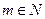 )
)
又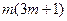 必为偶数,所以
必为偶数,所以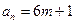 (
(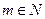 )满足
)满足
即 (
(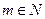 )时,
)时,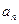 为整数;
为整数;
同理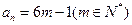 有
有 (
( )
)
也满足 ,即
,即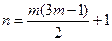 (
( )时,
)时,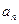 为整数;
为整数;
显然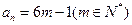 和
和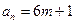 (
(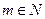 )是数列中的不同项;
)是数列中的不同项;
所以当 (
(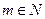 )和
)和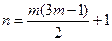 (
( )时,
)时,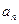 为整数;
为整数;
由 (
(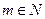 )有
)有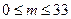 ,
,
由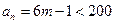 (
( )有
)有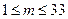 .
.
设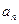 中满足
中满足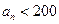 的所有整数项的和为
的所有整数项的和为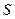 ,则
,则
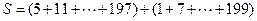
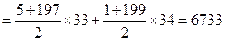
证明:(1)由已知有:
 ,从而
,从而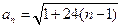 ,
,方法一:取
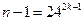 ,则
,则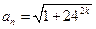 (
(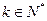 )
)用反证法证明这些
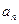 都是无理数.
都是无理数.假设
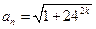 为有理数,则
为有理数,则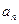 必为正整数,且
必为正整数,且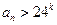 ,
,故
 .
.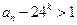 ,与
,与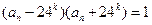 矛盾,
矛盾,所以
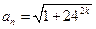 (
(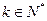 )都是无理数,即数列
)都是无理数,即数列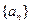 中有无穷多项为无理数;
中有无穷多项为无理数;方法二:因为
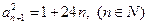 ,当
,当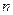 的末位数字是
的末位数字是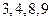 时,
时,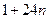 的末位数字是
的末位数字是 和
和 ,它不是整数的平方,也不是既约分数的平方,故此时
,它不是整数的平方,也不是既约分数的平方,故此时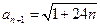 不是有理数,因这种
不是有理数,因这种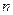 有无穷多,故这种无理项
有无穷多,故这种无理项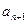 也有无穷多.
也有无穷多.(2) 要使
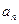 为整数,由
为整数,由 可知:
可知: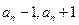 同为偶数,且其中一个必为3的倍数,所以有
同为偶数,且其中一个必为3的倍数,所以有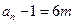 或
或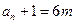
当
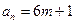 时,有
时,有 (
(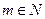 )
)又
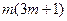 必为偶数,所以
必为偶数,所以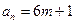 (
(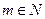 )满足
)满足
即
 (
(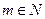 )时,
)时,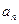 为整数;
为整数;同理
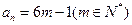 有
有 (
( )
)也满足
 ,即
,即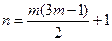 (
( )时,
)时,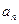 为整数;
为整数;显然
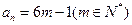 和
和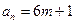 (
(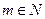 )是数列中的不同项;
)是数列中的不同项;所以当
 (
(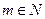 )和
)和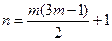 (
( )时,
)时,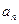 为整数;
为整数;由
 (
(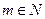 )有
)有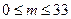 ,
,由
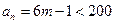 (
( )有
)有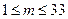 .
.设
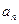 中满足
中满足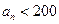 的所有整数项的和为
的所有整数项的和为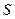 ,则
,则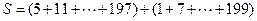

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
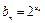 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.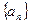 满足
满足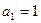 ,
,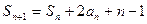 .
.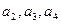 ;
;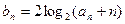 ,设
,设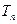 是数列
是数列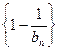 的前
的前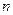 项积,若
项积,若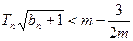 对
对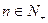 恒成立,求实数m的范围。
恒成立,求实数m的范围。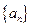 的通项公式
的通项公式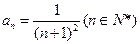 ,
, 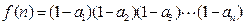 ,
,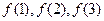 的值,由此推测
的值,由此推测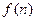 的计算公式,并用数学归纳法加以证明.
的计算公式,并用数学归纳法加以证明. }中,
}中, ,点
,点 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3…. ,求证数列
,求证数列 是等比数列;
是等比数列; 的通项;
的通项; 、
、 分别为数列
分别为数列 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出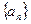 的通项公式为
的通项公式为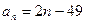 ,
,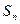 达到最小时,
达到最小时,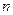 =______________.
=______________.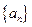 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列,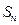 为
为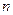 项和.
项和.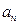 及
及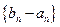 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列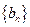 的通项公式及其前
的通项公式及其前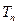 .
.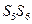 +15=0。
+15=0。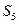 =5,求
=5,求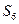 及a1;
及a1;