题目内容
设各项均为正数的数列 的前
的前 项和为
项和为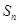 ,满足
,满足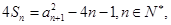 且
且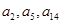 构成等比数列.
构成等比数列.
(1) 证明: ;
;
(2) 求数列 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 .
.
【答案】
(1)见解析 (2)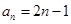 (3) 见解析
(3) 见解析
【解析】(1)当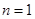 时,
时,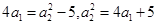 ,
,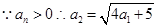
(2)当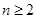 时,
时,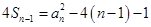 ,
,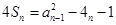 ,
,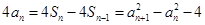
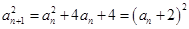 ,
,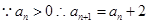
 当
当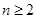 时,
时,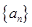 是公差
是公差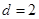 的等差数列.
的等差数列.
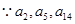 构成等比数列,
构成等比数列,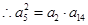 ,
,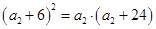 ,解得
,解得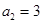 ,
,
由(1)可知,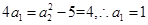
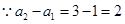

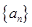 是首项
是首项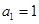 ,公差
,公差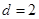 的等差数列.
的等差数列.
 数列
数列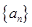 的通项公式为
的通项公式为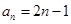 .
.
(3)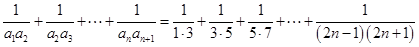
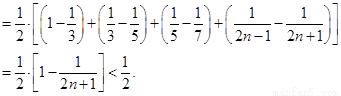
(1)直接将n换为1代入递推式求解;(2)借助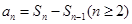 进行递推转化,进而构造数列
进行递推转化,进而构造数列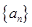 为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)采用列项相消法求和之后再证明.
为等差数列是解题的关键,考查了学生对式子的操作能力和转化能力.(3)采用列项相消法求和之后再证明.
【考点定位】本题考查数列的通项公式和数列求和问题,以及不等式的证明.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目