题目内容
已知焦点为F1(-1,0),F2(1,0)的椭圆经过点(1, ),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
(1)求 的范围;
的范围;
(2)若 与向量
与向量 共线,求
共线,求 的值及△AOB的外接圆方程.
的值及△AOB的外接圆方程.
解:(1)∵焦点为F1(-1,0),F2(1,0)的椭圆经过点(1, ),
),
∴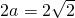 ,∴
,∴ ,
,
∵焦点为F1(-1,0),F2(1,0)
∴c=1
∴b2=1,所以椭圆的方程是 ,
,
直线方程y=k(x-1)代入椭圆的方程 ,消去y,化简为(2k2+1)x2-4k2x+2k2-2=0
,消去y,化简为(2k2+1)x2-4k2x+2k2-2=0
设A(x1,y1),B(x2,y2)
∴ =
= =
= (#)
(#)
令 =m,则
=m,则 ≥0,∴
≥0,∴ ,∴
,∴
当k不存在时, ,则
,则 =
=
综上, (6分)
(6分)
(2)
∵ 与向量
与向量 共线
共线
∴
∴
由韦达定理知k=0或k= 代入(#)得
代入(#)得 =-2或0
=-2或0
当 =-2时,A,O,B共线,不存在外接圆
=-2时,A,O,B共线,不存在外接圆
当 =0时,
=0时, ,外接圆直径为AB,圆心为(
,外接圆直径为AB,圆心为( ,-
,- ),
),
∴△AOB的外接圆方程为
分析:(1)利用焦点为F1(-1,0),F2(1,0)的椭圆经过点(1, ),结合椭圆的定义,可以求出椭圆的标准方程,再将直线方程与椭圆方程联立,将数量积用坐标表示,就可以求出
),结合椭圆的定义,可以求出椭圆的标准方程,再将直线方程与椭圆方程联立,将数量积用坐标表示,就可以求出 的范围;
的范围;
(2) 与向量
与向量 共线,及韦达定理,我们可以求出
共线,及韦达定理,我们可以求出 的值,再分类求出△AOB的外接圆方程即可.
的值,再分类求出△AOB的外接圆方程即可.
点评:椭圆的标准方程的确定,关键是确定椭圆的几何量,直线与椭圆的位置关系问题,通常要利用韦达定理,注意掌握技巧与方法.
 ),
),∴
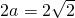 ,∴
,∴ ,
,∵焦点为F1(-1,0),F2(1,0)
∴c=1
∴b2=1,所以椭圆的方程是
 ,
,直线方程y=k(x-1)代入椭圆的方程
 ,消去y,化简为(2k2+1)x2-4k2x+2k2-2=0
,消去y,化简为(2k2+1)x2-4k2x+2k2-2=0设A(x1,y1),B(x2,y2)
∴
 =
= =
= (#)
(#) 令
 =m,则
=m,则 ≥0,∴
≥0,∴ ,∴
,∴
当k不存在时,
 ,则
,则 =
=
综上,
 (6分)
(6分)(2)

∵
 与向量
与向量 共线
共线∴

∴

由韦达定理知k=0或k=
 代入(#)得
代入(#)得 =-2或0
=-2或0当
 =-2时,A,O,B共线,不存在外接圆
=-2时,A,O,B共线,不存在外接圆当
 =0时,
=0时, ,外接圆直径为AB,圆心为(
,外接圆直径为AB,圆心为( ,-
,- ),
),
∴△AOB的外接圆方程为

分析:(1)利用焦点为F1(-1,0),F2(1,0)的椭圆经过点(1,
 ),结合椭圆的定义,可以求出椭圆的标准方程,再将直线方程与椭圆方程联立,将数量积用坐标表示,就可以求出
),结合椭圆的定义,可以求出椭圆的标准方程,再将直线方程与椭圆方程联立,将数量积用坐标表示,就可以求出 的范围;
的范围;(2)
 与向量
与向量 共线,及韦达定理,我们可以求出
共线,及韦达定理,我们可以求出 的值,再分类求出△AOB的外接圆方程即可.
的值,再分类求出△AOB的外接圆方程即可.点评:椭圆的标准方程的确定,关键是确定椭圆的几何量,直线与椭圆的位置关系问题,通常要利用韦达定理,注意掌握技巧与方法.

练习册系列答案
相关题目
 ),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点. 的范围;
的范围; 与向量
与向量 共线,求
共线,求 的值及△AOB的外接圆方程.
的值及△AOB的外接圆方程. ),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点.
),直线l过点F2与椭圆交于A、B两点,其中O为坐标原点. 的范围;
的范围; 与向量
与向量 共线,求
共线,求 的值及△AOB的外接圆方程.
的值及△AOB的外接圆方程.