题目内容
函数 的导数是
的导数是
- A.xlnx
- B.

- C.

- D.1
B
分析:直接根据导数的运算法求解即可得答案.
解答:∵ ∴y'=
∴y'= =
= =
=
故选B.
点评:本题主要考查导数的运算法则.属基础题.牢记法则是前提,准确计算是关键.
分析:直接根据导数的运算法求解即可得答案.
解答:∵
 ∴y'=
∴y'= =
= =
=
故选B.
点评:本题主要考查导数的运算法则.属基础题.牢记法则是前提,准确计算是关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目

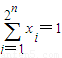 ,证明:
,证明: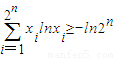
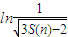 (i,n∈N*).
(i,n∈N*).