Question

已知正数数列{a_n}中,a₁=2.若关于x的方程x²-+=0(n∈N^*)有相等的实根,

(1)求a₂、a₃的值;

(2)求证:+…+＜(n∈N^*).

Answer 1

(1)解:由题意得Δ=a_n+1-2a_n-1=0得a_n+1=2a_n+1,得a₂=5,a₃=11.

(2)证明:由于a_n+1=2a_n+1=2(2a_n-1+1)+1=2²a_n-1+2+1

=2²(2a_n-2+1)+2+1=2³a_n-2+2²+2+1

=2ⁿa₁+2^n-1+2^n-2+…+2+1

=2ⁿ⁺¹+

=3·2ⁿ-1,

∴a_n+1=3·2^n-1,则

+…+

=(+++…+)

=·

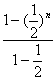
=［1-()ⁿ］

＜.

∴+…+＜.