题目内容
已知函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),则F(x)=[f-1(x)]2-f-1(x2)的值域为________.
[2,5]
分析:由函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),可求得b值,从而得到f(x)的解析式,根据f(x)的值域可得f-1(x)的定义域,进而可求得F(x)的定义域,F(x)=[f-1(x)]2-f-1(x2)=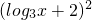 -(
-( +2)=
+2)=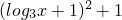 ,由log3x∈[0,1],即可求得F(x)的值域.
,由log3x∈[0,1],即可求得F(x)的值域.
解答:由函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),得32-b=1,解得b=2.
则f(x)=3x-2,f-1(x)=log3x+2,
F(x)=[f-1(x)]2-f-1(x2)=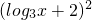 -(
-( +2)=
+2)=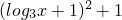 ,
,
由2≤x≤4得,f(x)∈[1,9].所以f-1(x)的定义域为[1,9],
由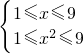 ,解得1≤x≤3,
,解得1≤x≤3,
所以F(x)的定义域为[1,3].
则log3x∈[0,1],1≤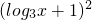 ≤4,2≤F(x)≤5.
≤4,2≤F(x)≤5.
所以函数F(x)的值域为[2,5].
故答案为:[2,5].
点评:本题考查函数解析式的求解及函数的值域问题,考查学生分析解决问题的能力.
分析:由函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),可求得b值,从而得到f(x)的解析式,根据f(x)的值域可得f-1(x)的定义域,进而可求得F(x)的定义域,F(x)=[f-1(x)]2-f-1(x2)=
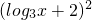 -(
-( +2)=
+2)=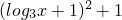 ,由log3x∈[0,1],即可求得F(x)的值域.
,由log3x∈[0,1],即可求得F(x)的值域.解答:由函数f(x)=3x-b(2≤x≤4)的图象过点(2,1),得32-b=1,解得b=2.
则f(x)=3x-2,f-1(x)=log3x+2,
F(x)=[f-1(x)]2-f-1(x2)=
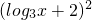 -(
-( +2)=
+2)=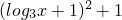 ,
,由2≤x≤4得,f(x)∈[1,9].所以f-1(x)的定义域为[1,9],
由
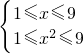 ,解得1≤x≤3,
,解得1≤x≤3,所以F(x)的定义域为[1,3].
则log3x∈[0,1],1≤
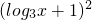 ≤4,2≤F(x)≤5.
≤4,2≤F(x)≤5.所以函数F(x)的值域为[2,5].
故答案为:[2,5].
点评:本题考查函数解析式的求解及函数的值域问题,考查学生分析解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |