题目内容
（本小题满分12分）
已知平面直角坐标系中，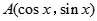
，
，
，
．
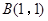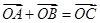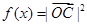（Ⅰ）求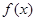
的最小正周期和对称中心；
（Ⅱ）求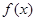在区间
上的单调递增区间．
【答案】
（Ⅰ）故最小正周期为
，对称中心是
；
（Ⅱ）
的递增区间为
和
。
【解析】
试题分析：(I)先根据向量的坐标的加法运算法则求出向量
的坐标，从而求出
从而可得其周期为,再利用正弦函数的对称中心
,可求出f(x)的对称中心.
(II)由正弦函数的单调增区间可知当
时单增,解此不等式可求出f(x)的单调增区间,然后给k赋值，可得f(x)在
上的增区间.
（Ⅰ）由题设知，
，……………………1分
，则
…………………2分
……………………………………4分
………………………………………………5分
故最小正周期为………………………………………………6分
对称中心横坐标满足
，即
对称中心是………………………………………………8分
（Ⅱ）当时单增，……………9分
即
……………………………………10分
又，故的递增区间为和………………………１２分
考点：向量的坐标运算，正弦型函数
的周期，对称中心，以及单调区间.
点评：掌握向量的坐标运算是解好本题的前题，理解并把握的周期，对称中心，对称轴，以及单调区间的求法是解题的关键.
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
