Question

已知A(3,0)、B(0,3)、C(cosα,sinα),

(1)若·=-1,求sin2α的值;

(2)若|+|=,且α∈(0,π),求与的夹角.

Answer 1

解：(1) =(cosα-3,sinα), =(cosα,sinα-3).

    由·=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.

∴cosα+sinα=,两边平方,得1+sin2α=,∴sin2α=-.

(2) + =(3+cosα,sinα),

∴(3+cosα)²+sin²α=13.

∴cosα=.

∵α∈(0,π),

∴α=,sinα=.

∴C(,),·=.

    设与的夹角为θ,

cosθ===.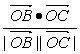

∴θ=,即与的夹角为.