题目内容
已知焦点在x轴上的椭圆 F1,F2是它的两个焦点,若椭圆上存在点P,使
F1,F2是它的两个焦点,若椭圆上存在点P,使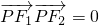 ,则b的取值范围是 ________.
,则b的取值范围是 ________.
(0, ]
]
分析:先证:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2.记∠F1PF2=θ,
|PF1|=r1,|PF2|=r2,cosθ=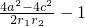 推出cosθ≥
推出cosθ≥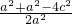 =cos∠F1BF2,即∠F1PF2≤∠F1BF2.
=cos∠F1BF2,即∠F1PF2≤∠F1BF2.
利用结论,题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,推出b∈(0, ].
].
解答:先证一个结论:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2.记∠F1PF2=θ,
|PF1|=r1,|PF2|=r2,cosθ=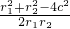 =
=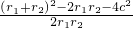 =
=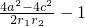
又r1r2≤(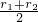 )2=a2,∴cosθ≥
)2=a2,∴cosθ≥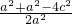 =cos∠F1BF2,当且仅当r1=r2时等号成立,
=cos∠F1BF2,当且仅当r1=r2时等号成立,
即∠F1PF2≤∠F1BF2.题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,即
cos∠F1BO≤ 等价于b≤
等价于b≤ a=
a= ,∴b∈(0,
,∴b∈(0, ].
].
故答案为:(0, ].
].
点评:本题考查椭圆的应用,考查分析问题解决问题的能力,计算能力逻辑思维能力,是难题,考查转化思想.
 ]
]分析:先证:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2.记∠F1PF2=θ,
|PF1|=r1,|PF2|=r2,cosθ=
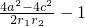 推出cosθ≥
推出cosθ≥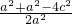 =cos∠F1BF2,即∠F1PF2≤∠F1BF2.
=cos∠F1BF2,即∠F1PF2≤∠F1BF2.利用结论,题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,推出b∈(0,
 ].
].解答:先证一个结论:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2.记∠F1PF2=θ,
|PF1|=r1,|PF2|=r2,cosθ=
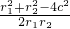 =
=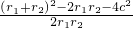 =
=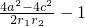
又r1r2≤(
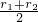 )2=a2,∴cosθ≥
)2=a2,∴cosθ≥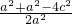 =cos∠F1BF2,当且仅当r1=r2时等号成立,
=cos∠F1BF2,当且仅当r1=r2时等号成立,即∠F1PF2≤∠F1BF2.题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,即
cos∠F1BO≤
 等价于b≤
等价于b≤ a=
a= ,∴b∈(0,
,∴b∈(0, ].
].故答案为:(0,
 ].
].点评:本题考查椭圆的应用,考查分析问题解决问题的能力,计算能力逻辑思维能力,是难题,考查转化思想.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目

 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( ) 和椭圆弧
和椭圆弧
