题目内容
给出下列命题:①已知
 ,
, 为互相垂直的单位向量,
为互相垂直的单位向量, =
= -2
-2 ,
, =
= +λ
+λ ,且
,且 ,
, 的夹角为锐角,则实数λ的取值范围是(-∞,
的夹角为锐角,则实数λ的取值范围是(-∞, );
);②若某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是
 =10x+200;
=10x+200;③若x1,x2,x3,x4的方差为3,则3(x1-1),3(x2-1),3(x3-1)),3(x4-1)的方差为27;
④设a,b,C分别为△ABC的角A,B,C的对边,则方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°.
上面命题中,假命题的序号是 (写出所有假命题的序号).
【答案】分析:根据λ=-2时, ,
, 同向,可判断①的真假;
同向,可判断①的真假;
根据回归系数符号与相关性的关系,可判断②的真假;
根据数据增加a,数据的方差不变,数据扩大a倍,数据的方差扩大a2倍,可判断③的真假;
根据充要条件的定义,分别判断A=90°时设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根和设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根时,A=90°的真假,可判断④的真假.
解答:解:∵λ=-2时, ,
, 同向,
同向, ,
, 的夹角为0,不是锐角,故①错误;
的夹角为0,不是锐角,故①错误;
若某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程的回归系数 <0,不可能是
<0,不可能是 =10x+200,故②错误
=10x+200,故②错误
若x1,x2,x3,x4的方差为3,则(x1-1),(x2-1),(x3-1)),(x4-1)的方差为3,3(x1-1),3(x2-1),3(x3-1)),3(x4-1)的方差为3×32=27,故③正确;
当A=90°时,a2=b2+c2,则x2+2ax+b2=0?x2+2ax+a2-c2=0?[x+(a+c)][x+(a-c)]=0,该方程有两根x1=-(a+c),x2=-(a-c).
同样,x2+2cx-b2=0?[x+(c+a)][x+(c-a)]=0,该方程亦有两根x3=-(c+a),x4=-(c-a),显然x1=x3,两方程有公共根.
设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根为m,则x2+2ax+b2=0加x2+2cx-b2=0得m=-(a+c).m=0(舍去).将m=-(a+c)代入(1)式,得[-(a+c)]2+2a•[-(a+c)]+b2=0,整理得a2=b2+c2,即A=90°,故④正确;
故答案为:①②
点评:本题又命题的真假判断为载体考查了向量的数量积运算,相关关系,方差的变化,充要条件等基础知识,难度中档.
 ,
, 同向,可判断①的真假;
同向,可判断①的真假;根据回归系数符号与相关性的关系,可判断②的真假;
根据数据增加a,数据的方差不变,数据扩大a倍,数据的方差扩大a2倍,可判断③的真假;
根据充要条件的定义,分别判断A=90°时设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根和设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根时,A=90°的真假,可判断④的真假.
解答:解:∵λ=-2时,
 ,
, 同向,
同向, ,
, 的夹角为0,不是锐角,故①错误;
的夹角为0,不是锐角,故①错误;若某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程的回归系数
 <0,不可能是
<0,不可能是 =10x+200,故②错误
=10x+200,故②错误若x1,x2,x3,x4的方差为3,则(x1-1),(x2-1),(x3-1)),(x4-1)的方差为3,3(x1-1),3(x2-1),3(x3-1)),3(x4-1)的方差为3×32=27,故③正确;
当A=90°时,a2=b2+c2,则x2+2ax+b2=0?x2+2ax+a2-c2=0?[x+(a+c)][x+(a-c)]=0,该方程有两根x1=-(a+c),x2=-(a-c).
同样,x2+2cx-b2=0?[x+(c+a)][x+(c-a)]=0,该方程亦有两根x3=-(c+a),x4=-(c-a),显然x1=x3,两方程有公共根.
设方程x2+2ax+b2=0与x2+2cx-b2=0的公共根为m,则x2+2ax+b2=0加x2+2cx-b2=0得m=-(a+c).m=0(舍去).将m=-(a+c)代入(1)式,得[-(a+c)]2+2a•[-(a+c)]+b2=0,整理得a2=b2+c2,即A=90°,故④正确;
故答案为:①②
点评:本题又命题的真假判断为载体考查了向量的数量积运算,相关关系,方差的变化,充要条件等基础知识,难度中档.

练习册系列答案
相关题目
 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.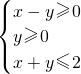 ”是“|2y-x|≤2”的充分不必要条件.
”是“|2y-x|≤2”的充分不必要条件.