Question

已知f（x）=ln（x+1），，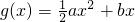
（Ⅰ）若b=2，且h（x）=f（x-1）-g（x）存在单调递减区间，求a的取值范围；
（Ⅱ）若a=0，b=1时，求证：f（x）-g（x）≤0对于x∈（-1，+∞）恒成立；
（III）证明：若0＜x＜y，则．

Answer 1

解：（Ⅰ）b=2时，
∵h（x）有单调递减区间，∴h′（x）＜0有解，即有解，
∵x＞0，∴ax²+2x-1＞0有解，．（2分）
①a≥0时合题意
②a＜0时，△=4+4a＞0，即a＞-1，
∴a的取值范围是（-1，+∞）．（4分）
（Ⅱ）设?（x）=f（x）-g（x）=ln（x+1）-x
．

x	（-1，0）	0	（0，+∞）
?′（x）	+	0	-
?（x）	↗	最大值	↘

∵当x=0时，?（x）有最大值0∴?（x）≤0恒成立．
即f（x）-g（x）≤0对于x∈（-1，+∞）恒成立．（8分）
（III）
=
=．（10分）
当0＜x＜y时，，
由（2）知．（12分）
等号在，即x=y时成立．
而y＞x＞0，所以成立．（14分）
分析：（I）求出h（x）的导函数，由于h（x）存在单调递减区间等价于h′（x）＜0有解，通过对二次项系数的讨论，求出a的范围．
（II）构造函数φ（x），求出φ（x）的导数，列出x，φ′（x），φ（x）的变化情况表，求出φ（x）的最大值，证出不等式．
（III）作差，利用对数的运算性质化简差，利用（II）的结论，证出要证的不等式．
点评：解决不等式恒成立问题与不等式有解问题常转化为求函数的相应的最值问题；证明不等式成立也常常通过构造函数，转化为求函数的最值．