Question

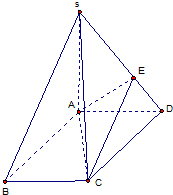（2012•陕西三模）如图，在四棱锥S-ABCD中，底面ABCD为平行四边形，SA⊥底面ABCD，AB=2，AD=1，SB=

7

，∠BAD=120°，E在棱SD上．
（Ⅰ）当SE=3ED时，求证：SD⊥平面AEC；
（Ⅱ）当二面角S-AC-E的大小为30°时，求直线AE与平面CDE所成角的正弦值．

Answer 1

分析：先根据条件得到CA⊥AD，再结合SA⊥平面ABCD建立空间直角坐标系，求出各点的坐标；
（Ⅰ）利用SE=3ED求出点E的坐标，进而得到向量的数量积为0即可证明结论；
（Ⅱ）先根据二面角S-AC-E的大小为30°求出点E的位置，进而求出向量AE的坐标以及平面CDE法向量的坐标，最后代入线面角的计算公式即可．

解答：解：在平行四边形ABCD中，∵AB=2，AD=1，∠BAD=120°，
∴CA⊥AD，又SA⊥平面ABCD，
∴以A为坐标原点，AC，AD，AS所在直线为x轴，y轴，z轴建立空间直角坐标系，
则A（0，0，0），C(

3

，0，0)，D（0，1，0）
∵SB=

7

，
∴SA=

3

∴S(0，0，

3

)
（Ⅰ）∵SE=3ED
∴E(0，

3

4

，

3

4

)
∵

SD

=(0，1，-

3

)，

AE

=(0，

3

4

，

3

4

)，

AC

=(

3

，0，0)
∴

SD

•

AE

=0，

SD

•

AC

=0
∴SD⊥平面AEC
（Ⅱ）∵AC⊥平面SAD，SA⊥底面ABCD，
∴AC⊥AE，AC⊥SA
∴∠SAE为二面角S-AC-E的平面角，即∠SAE=30°，此时E为SD的中点E(0，

1

2

，

3

2

)
设平面CDE的法向量为

n

=(x，y，z)
计算可得

n

=(1，

3

，1)，

AE

=(0，

1

2

，

3

2

)
∴cos?

n

，

AE

＞=

15

5

即直线AE与平面CDE所成角的正弦值为

15

5

．

点评：本题主要考察用空间向量求直线与平面的夹角．解题的关键是要用的点的坐标比较多，写起来比较繁琐，注意不要出错．