题目内容
给出下列四个命题:
①若|x-lgx|<x+|lgx|成立,则x>1;
②若p=a+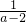 (a>2),q=
(a>2),q=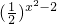 (x∈R),则p>q,
(x∈R),则p>q,
③已知 =|
=| |=2,
|=2, 与
与 的夹角为
的夹角为 ,则
,则 +
+ 在
在 上的投影为3;
上的投影为3;
④已知f(x)=asinx-bcosx,(a,b∈R)在x= 处取得最小值,则f(
处取得最小值,则f( -x)=-f(x).
-x)=-f(x).
其中正确命题的序号是________.(把你认为正确的命题的序号都填上)
①③④
分析:①若|x-lgx|<x+|lgx|成立,则 可求x的范围②利用基本不等式可求p=a+
可求x的范围②利用基本不等式可求p=a+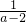 =a-2+
=a-2+ ≥4,而q=
≥4,而q=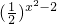
 ,则可比较p,q的大小③求
,则可比较p,q的大小③求 +
+ 与
与 的夹角θ及|
的夹角θ及| |,根据投影的定义可得,
|,根据投影的定义可得, +
+ 在
在 上的投影为|
上的投影为| |cosθ,代入可求④由f(x)=asinx-bcosx在x=
|cosθ,代入可求④由f(x)=asinx-bcosx在x= 处取得最小值,可得a=-b,代入到函数中可得f(x)=asinx+acosx=
处取得最小值,可得a=-b,代入到函数中可得f(x)=asinx+acosx= 把f(
把f( -x)代入检验
-x)代入检验
解答:①若|x-lgx|<x+|lgx|成立,则 ?x>1,①正确
?x>1,①正确
②p=a+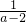 =a-2+
=a-2+ ≥4(a>2),q=
≥4(a>2),q=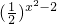
 ,则p≥q,②错误
,则p≥q,②错误
③由 =|
=| |=2,
|=2, 与
与 的夹角为
的夹角为 可得
可得 +
+ 与
与 的夹角为投影为30°,根据投影的定义可得,
的夹角为投影为30°,根据投影的定义可得, +
+ 在
在 上的投影为
上的投影为
| |cos30°=2
|cos30°=2 ,③正确
,③正确
④f(x)=asinx-bcosx,在x= 处取得最小值,可得a=-b,则f(x)=asinx+acosx=
处取得最小值,可得a=-b,则f(x)=asinx+acosx=
,f( -x)═
-x)═ =-f(x),④正确
=-f(x),④正确
故答案为:①③④
点评:本题是一道把不等式的性质及利用基本不等式求解最值、向量的夹角及投影的定义的考查、三角函数的性质等知识的综合运用,此类问题在高考中一般会出现在填空的压轴题,要求考生能够熟练的运用所学的知识解决综合问题.
分析:①若|x-lgx|<x+|lgx|成立,则
 可求x的范围②利用基本不等式可求p=a+
可求x的范围②利用基本不等式可求p=a+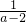 =a-2+
=a-2+ ≥4,而q=
≥4,而q=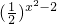
 ,则可比较p,q的大小③求
,则可比较p,q的大小③求 +
+ 与
与 的夹角θ及|
的夹角θ及| |,根据投影的定义可得,
|,根据投影的定义可得, +
+ 在
在 上的投影为|
上的投影为| |cosθ,代入可求④由f(x)=asinx-bcosx在x=
|cosθ,代入可求④由f(x)=asinx-bcosx在x= 处取得最小值,可得a=-b,代入到函数中可得f(x)=asinx+acosx=
处取得最小值,可得a=-b,代入到函数中可得f(x)=asinx+acosx= 把f(
把f( -x)代入检验
-x)代入检验解答:①若|x-lgx|<x+|lgx|成立,则
 ?x>1,①正确
?x>1,①正确②p=a+
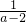 =a-2+
=a-2+ ≥4(a>2),q=
≥4(a>2),q=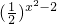
 ,则p≥q,②错误
,则p≥q,②错误③由
 =|
=| |=2,
|=2, 与
与 的夹角为
的夹角为 可得
可得 +
+ 与
与 的夹角为投影为30°,根据投影的定义可得,
的夹角为投影为30°,根据投影的定义可得, +
+ 在
在 上的投影为
上的投影为|
 |cos30°=2
|cos30°=2 ,③正确
,③正确④f(x)=asinx-bcosx,在x=
 处取得最小值,可得a=-b,则f(x)=asinx+acosx=
处取得最小值,可得a=-b,则f(x)=asinx+acosx=
,f(
 -x)═
-x)═ =-f(x),④正确
=-f(x),④正确故答案为:①③④
点评:本题是一道把不等式的性质及利用基本不等式求解最值、向量的夹角及投影的定义的考查、三角函数的性质等知识的综合运用,此类问题在高考中一般会出现在填空的压轴题,要求考生能够熟练的运用所学的知识解决综合问题.

练习册系列答案
相关题目