题目内容
函数 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
A
解析试题分析:因为函数 ,那么要使得原式有意义,则满足
,那么要使得原式有意义,则满足 ,得到其定义域为
,得到其定义域为 ,选A.
,选A.
考点:本试题主要考查了函数定义域的求解。
点评:解决该试题的关键是理解偶次根式下被开方数为非负数,对数真数大于零的特点,进而求解得到。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列两个函数完全相同的是( )
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有 <0,则( )
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
下列函数中,在其定义域内既是奇函数又是增函数的是( )
A. | B. | C.y=x3 | D. |
函数 的图象如图所示,其中
的图象如图所示,其中 为常数,则下列结论正确的是
为常数,则下列结论正确的是
A. | B. | C. | D. |
对实数a和b,定义运算“⊕”:a⊕b= 设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
设函数f(x)=(x2-2)⊕(x-x2),x∈R,若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是
A.(-∞,-2]∪ | B.(-∞,-2]∪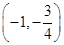 |
C.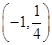 ∪ ∪ | D.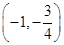 ∪ ∪ |
 与
与 的图象是 ( )
的图象是 ( )




