题目内容
(本题满分15分)已知函数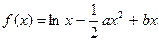
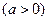 且导数
且导数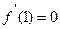 .
.
(Ⅰ)试用含有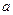 的式子表示
的式子表示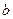 ,并求
,并求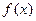 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点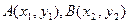 ,如果在函数图象上存在点
,如果在函数图象上存在点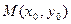 (其中
(其中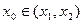 )使得点
)使得点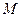 处的切线
处的切线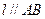 ,则称
,则称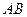 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当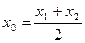 时,又称
时,又称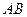 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数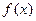 上是否存在两点
上是否存在两点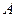 、
、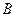 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出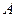 、
、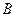 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
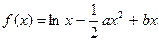
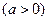 且导数
且导数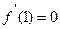 .
.(Ⅰ)试用含有
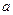 的式子表示
的式子表示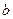 ,并求
,并求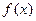 单调区间; (II)对于函数图象上的不同两点
单调区间; (II)对于函数图象上的不同两点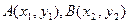 ,如果在函数图象上存在点
,如果在函数图象上存在点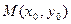 (其中
(其中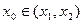 )使得点
)使得点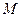 处的切线
处的切线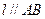 ,则称
,则称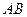 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当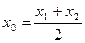 时,又称
时,又称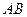 存在“中值伴侣切线”.试问:在函数
存在“中值伴侣切线”.试问:在函数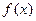 上是否存在两点
上是否存在两点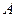 、
、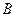 使得它存在“中值伴侣切线”,若存在,求出
使得它存在“中值伴侣切线”,若存在,求出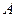 、
、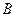 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.(Ⅰ)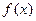 在
在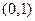 上单调递增,在
上单调递增,在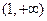 上单调递减 (Ⅱ) 不存在
上单调递减 (Ⅱ) 不存在
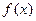 在
在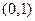 上单调递增,在
上单调递增,在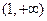 上单调递减 (Ⅱ) 不存在
上单调递减 (Ⅱ) 不存在(Ⅰ)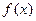 的定义域为
的定义域为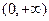
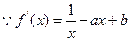 ,
,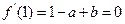 得:
得: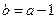 …2分 代入:
…2分 代入: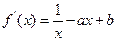 得
得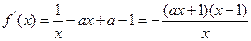
当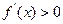 时,
时,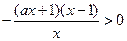 由
由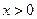 ,得
,得 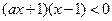
又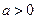
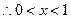 即
即 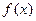 在
在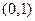 上单调递增 ……4分
上单调递增 ……4分
当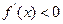 时,
时,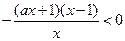 由
由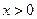 ,得
,得 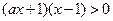
又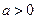
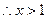 即
即 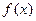 在
在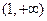 上单调递减
上单调递减
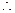
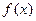 在
在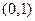 上单调递增,在
上单调递增,在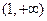 上单调递减 ……6分
上单调递减 ……6分
(II) 在函数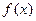 上不存在两点A、B使得它存在“中值伴侣切线”。
上不存在两点A、B使得它存在“中值伴侣切线”。
假设存在两点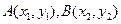 ,不妨设
,不妨设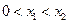 ,则
,则
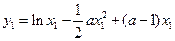 ,
,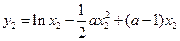
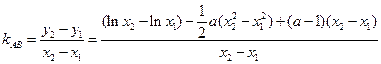
=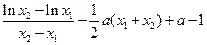 ……8分
……8分
在函数图象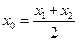 处的切线斜率
处的切线斜率
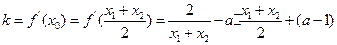
得: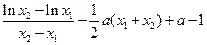
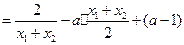
化简得: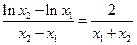 ,
, 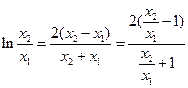 …… 11分
…… 11分
令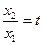 ,则
,则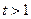 ,上式化为:
,上式化为: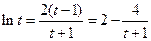 ,即
,即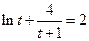
若令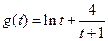 ,
,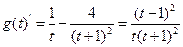
由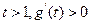 ,
, 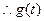 在
在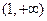 上单调递增,
上单调递增,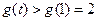
这表明在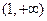 内不存在
内不存在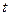 ,使得
,使得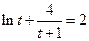 ……14分
……14分
综上所述,在函数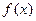 上不存在两点A、B使得它存在“中值伴侣切线”。 …15分
上不存在两点A、B使得它存在“中值伴侣切线”。 …15分
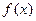 的定义域为
的定义域为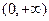
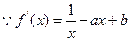 ,
,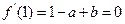 得:
得: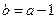 …2分 代入:
…2分 代入: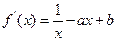 得
得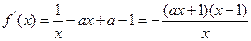
当
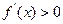 时,
时,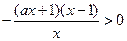 由
由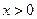 ,得
,得 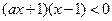
又
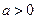
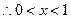 即
即 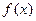 在
在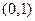 上单调递增 ……4分
上单调递增 ……4分当
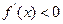 时,
时,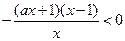 由
由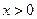 ,得
,得 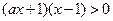
又
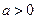
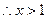 即
即 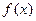 在
在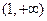 上单调递减
上单调递减 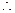
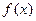 在
在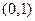 上单调递增,在
上单调递增,在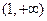 上单调递减 ……6分
上单调递减 ……6分(II) 在函数
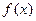 上不存在两点A、B使得它存在“中值伴侣切线”。
上不存在两点A、B使得它存在“中值伴侣切线”。 假设存在两点
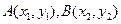 ,不妨设
,不妨设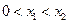 ,则
,则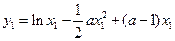 ,
,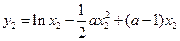
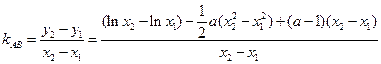
=
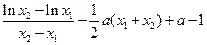 ……8分
……8分在函数图象
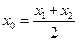 处的切线斜率
处的切线斜率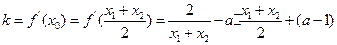
得:
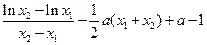
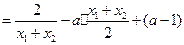
化简得:
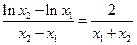 ,
, 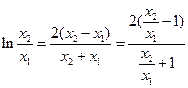 …… 11分
…… 11分令
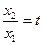 ,则
,则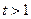 ,上式化为:
,上式化为: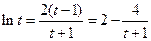 ,即
,即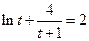
若令
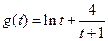 ,
,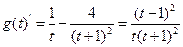
由
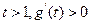 ,
, 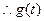 在
在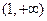 上单调递增,
上单调递增,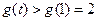
这表明在
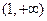 内不存在
内不存在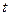 ,使得
,使得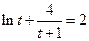 ……14分
……14分综上所述,在函数
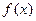 上不存在两点A、B使得它存在“中值伴侣切线”。 …15分
上不存在两点A、B使得它存在“中值伴侣切线”。 …15分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目


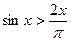


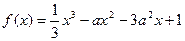 (a>0)
(a>0)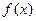 的单调区间,极大值,极小值
的单调区间,极大值,极小值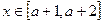 时,恒有
时,恒有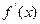 >
>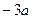 ,求实数a的取值范围
,求实数a的取值范围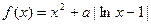 .(Ⅰ)当
.(Ⅰ)当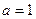 时,求曲线
时,求曲线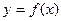 在
在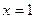 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当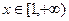 时,求函数
时,求函数 的最小值.
的最小值.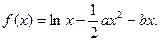 (1)当
(1)当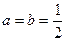 时,求
时,求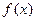 的最大值;(2)令
的最大值;(2)令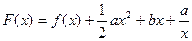 ,(0
,(0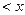 ≤3),其图象上任意一点
≤3),其图象上任意一点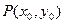 处切线的斜率
处切线的斜率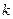 ≤
≤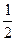 恒成立,求实数
恒成立,求实数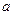 的取值范围;(3)当
的取值范围;(3)当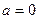 ,
,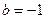 ,方程
,方程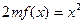 有唯一实数解,求正数
有唯一实数解,求正数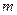 的值。
的值。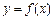 是二次函数,方程
是二次函数,方程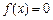 有两个相等实根,且
有两个相等实根,且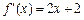 ,求
,求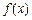 的表达式.
的表达式.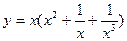 的导数;
的导数;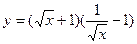 的导数;
的导数;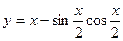 的导数;
的导数;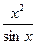 的导数;
的导数;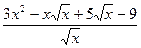 的导数。
的导数。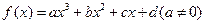 ,定义:设
,定义:设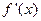 是函数
是函数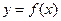 的导函数
的导函数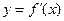 的导数,若
的导数,若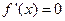 有实数解
有实数解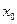 ,则称点
,则称点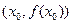 为函数
为函数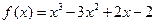 ,请解答下列问题:
,请解答下列问题: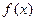 的“拐点”A的坐标;
的“拐点”A的坐标;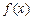 的导函数
的导函数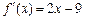 ,且
,且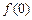 的值为整数,当
的值为整数,当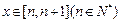 时,
时, 。
。