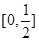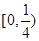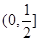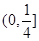题目内容
定义域为R的函数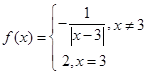 ,若关于
,若关于 的方程
的方程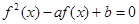 有3个不同实数解
有3个不同实数解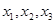 ,且
,且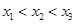 ,则下列说法错误的是( )
,则下列说法错误的是( )
A.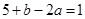 | B.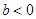 |
C.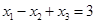 | D.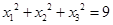 |
D
解析试题分析:若关于 的方程
的方程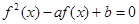 有3个不同实数根,则
有3个不同实数根,则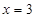 是方程的一个解,所以把
是方程的一个解,所以把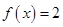 代入方程得
代入方程得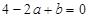 ,则有
,则有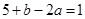 ,故A正确;又由
,故A正确;又由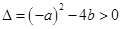 可得
可得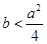 ,所以B正确;因为函数
,所以B正确;因为函数 是关于直线
是关于直线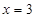 对称,且函数值
对称,且函数值 是方程的根,所以方程的另两根必关于直线
是方程的根,所以方程的另两根必关于直线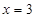 对称,又因为
对称,又因为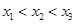 ,则必有
,则必有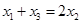 ,且
,且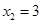 ,所以C正确,而D选项的结论是错,故答案选D.
,所以C正确,而D选项的结论是错,故答案选D.
考点:1.函数图像的对称性;2.方程根与系数的关系.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
若函数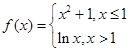 则
则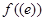 (e为自然对数的底数)=( )
(e为自然对数的底数)=( )
| A.0 | B.1 | C.2 | D.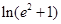 |
方程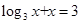 的解所在的区间为
的解所在的区间为
A.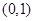 | B.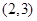 | C.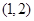 | D.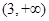 |
设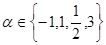 ,则使函数
,则使函数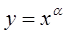 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有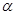 的值为( )
的值为( )
| A.-1,3 | B.-1,1 | C.1,3 | D.-1,1,3 |
设 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
已知关于 的方程
的方程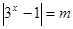 有一解,则
有一解,则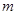 的取值范围为( )
的取值范围为( )
A.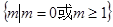 | B.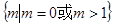 | C.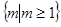 | D.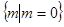 |
设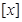 表示不大于
表示不大于 的最大整数,则函数
的最大整数,则函数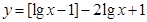 的零点之积为( )
的零点之积为( )
A.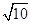 | B.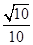 | C.-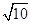 | D.0 |
若函数 ,则
,则 ( )
( )
A.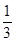 | B.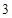 | C.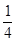 | D.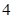 |
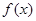 的定义域为
的定义域为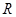 ,
,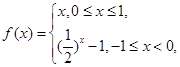 且对于任意的
且对于任意的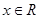 都有
都有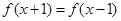 ,若在区间
,若在区间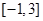 上函数
上函数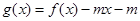 恰有四个不同零点,则实数
恰有四个不同零点,则实数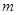 的取值范围为( )
的取值范围为( )