题目内容
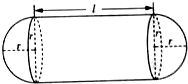
 如图,某公司制造一种海上用的“浮球”,它是由两个半球和一个圆柱筒组成.其中圆柱的高为2米,球的半径r为0.5米.
如图,某公司制造一种海上用的“浮球”,它是由两个半球和一个圆柱筒组成.其中圆柱的高为2米,球的半径r为0.5米.(1)这种“浮球”的体积是多少立方米(结果精确到0.1m3)?
(2)假设该“浮球”的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为20元,半球形部分每平方米建造费用为30元.求该“浮球”的建造费用(结果精确到1元).
分析:(1)根据球的半径得到上下两个半球的体积之和,再由柱体体积公式算出圆柱筒的体积,相加即得该“浮球”的体积大小;
(2)计算球的表面积公式和圆柱侧面积公式,结合条件,即可得到结论.
(2)计算球的表面积公式和圆柱侧面积公式,结合条件,即可得到结论.
解答:解:(1)∵球的半径r为0.5米,
∴两个半球的体积之和为V球=
πr3=
π•
=
πm3,
∵圆柱的高为2米,
∴V圆柱=πr2•h=π×
×2=
πm3,
∴该“浮球”的体积是:V=V球+V圆柱=
π≈2.1m3;
(2)圆柱筒的表面积为2πrh=2πm2;两个半球的表面积为4πr2=πm2,
∵圆柱形部分每平方米建造费用为20元,半球形部分每平方米建造费用为30元,
∴该“浮球”的建造费用为2π×20+π×30=70π≈220元.
∴两个半球的体积之和为V球=
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 8 |
| 1 |
| 6 |
∵圆柱的高为2米,
∴V圆柱=πr2•h=π×
| 1 |
| 4 |
| 1 |
| 2 |
∴该“浮球”的体积是:V=V球+V圆柱=
| 2 |
| 3 |
(2)圆柱筒的表面积为2πrh=2πm2;两个半球的表面积为4πr2=πm2,
∵圆柱形部分每平方米建造费用为20元,半球形部分每平方米建造费用为30元,
∴该“浮球”的建造费用为2π×20+π×30=70π≈220元.
点评:本题给出由两个半球和一个圆柱筒接成的“浮球”,计算了它的表面积和体积,着重考查了球、圆柱的表面积公式和体积公式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,某公司制造一种海上用的“浮球”,它是由两个半球和一个圆柱筒组成.其中圆柱的高为2米,球的半径r为0.5米.
如图,某公司制造一种海上用的“浮球”,它是由两个半球和一个圆柱筒组成.其中圆柱的高为2米,球的半径r为0.5米.