题目内容
在Rt△ABC中，∠A=30°，过直角顶点C作射线CM交线段AB于M，求使|AM|＞|AC|的概率．
分析：由于过直角顶点C在∠ACB内部任作一射线CM，故可以认为所有可能结果的区域为∠ACB，可将事件A构成的区域为∠ACC′，以角度为“测度”加以计算，可得本题答案．
解答：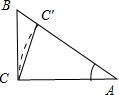
解：在AB上取AC′=AC，则∠ACC′=
=75°．
则所有可能结果的区域为∠ACB，事件A构成的区域为∠ACC′．
∵∠ACB=90°，∠ACC′=75°．
∴|AM|＞|AC|的概率为P=
=
．
解：在AB上取AC′=AC，则∠ACC′=| 180°-30° |
| 2 |
则所有可能结果的区域为∠ACB，事件A构成的区域为∠ACC′．
∵∠ACB=90°，∠ACC′=75°．
∴|AM|＞|AC|的概率为P=
| 90°-75° |
| 90° |
| 1 |
| 6 |
点评：本题给出Rt△ABC，求|AM|＞|AC|的概率．着重考查了几何概型及其应用的知识，属于中档题．解题时注意题意中的“测度”，准确把握“测度”是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于D，且AD：BD=9：4，则AC：BC=
（几何证明选讲选做题）