题目内容
已知函数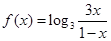 .
.
(1)证明函数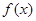 的图像关于点
的图像关于点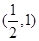 对称;
对称;
(2)若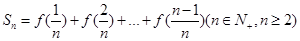 ,求
,求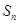 ;
;
(3)在(2)的条件下,若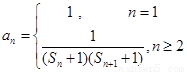
 ,
,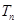 为数列
为数列 的前
的前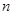 项和,若
项和,若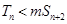 对一切
对一切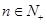 都成立,试求实数
都成立,试求实数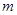 的取值范围.
的取值范围.
【答案】
(1)函数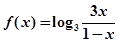 的定义域为
的定义域为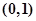 ,设
,设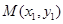 、
、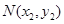 是函数
是函数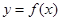 图像上的两点, 其中
图像上的两点, 其中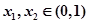 且
且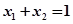 ,则有
,则有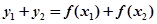

 ,因此函数图像关于点
,因此函数图像关于点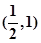 对称(2)
对称(2)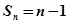 (3)
(3)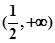
【解析】
试题分析:(1)
证明:因为函数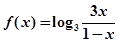 的定义域为
的定义域为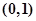 , 设
, 设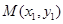 、
、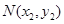 是函数
是函数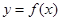 图像上的两点, 其中
图像上的两点, 其中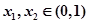 且
且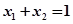 ,
,
则有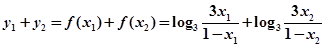

因此函数图像关于点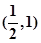 对称
4分
对称
4分
(2)由(1)知当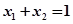 时,
时,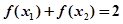
 ①
① 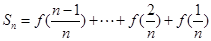 ②
②
①+②得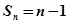 8分
8分
(3)当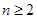 时,
时,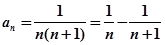
当 时,
时,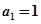 ,
, 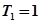
当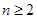 时,
时,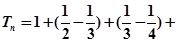
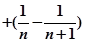 =
= 
∴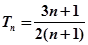 (
(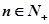 )
)
又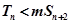 对一切
对一切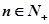 都成立,即
都成立,即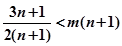 恒成立
恒成立
∴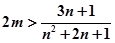 恒成立,又设
恒成立,又设 ,
,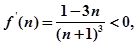 所以
所以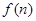 在
在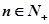 上递减,所以
上递减,所以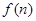 在
在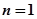 处取得最大值
处取得最大值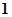
∴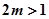 ,即
,即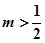
所以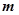 的取值范围是
的取值范围是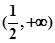 12分
12分
考点:函数对称性,求最值与数列求和
点评:证明函数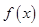 关于点
关于点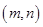 对称只需证明
对称只需证明 ,第二问数列求和结合通项的特点采用倒序相加法,第三问将不等式恒成立转化为求函数最值,进而可借助于导数求解
,第二问数列求和结合通项的特点采用倒序相加法,第三问将不等式恒成立转化为求函数最值,进而可借助于导数求解

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |