题目内容
【题目】已知![]() .
.
(1)若![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值;
的值;
(2)当![]() 时,若
时,若![]() ,都有
,都有![]() 成立,求实数
成立,求实数
![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用![]() 是函数
是函数![]() 的极值点,求出
的极值点,求出![]() ,即可求出
,即可求出![]() 的值;(2)对
的值;(2)对![]() 进行配方,讨论其最值问题,根据题意
进行配方,讨论其最值问题,根据题意![]() ,总有
,总有![]() 成立,只要要求
成立,只要要求![]() ,即可,从而求出
,即可,从而求出![]() 的范围.
的范围.
试题解析:(1)![]() ,又因为
,又因为![]() 是极值点,则
是极值点,则![]() ,则
,则![]() ,经检验,当
,经检验,当![]() 时,
时, ![]() 是
是![]() 极值点,故名满足题意.
极值点,故名满足题意.
(2)当a=2时,f(x)=2x-![]() -5ln x,
-5ln x,
f ′(x)=![]() ,
,
∴当x∈(0, ![]() )时,f ′ (x)>0,f(x)单调递增;
)时,f ′ (x)>0,f(x)单调递增;
当x∈(![]() ,1)时,f ′(x)<0,f(x)单调递减.
,1)时,f ′(x)<0,f(x)单调递减.
∴在(0,1)上,f(x)max=f(![]() )=-3+5ln2.
)=-3+5ln2.
又“x1∈(0,1),x2∈[1,2],都有f(x1)≥g(/span>x2)成立”等价于“f(x)在(0,1)上的最大值不小于g(x)在[1,2]上的最大值”,而g(x)在[1,2]上的最大值为max{g(1),g(2)},
∴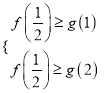 ,即
,即![]() ,
,
解得m≥8-5ln 2.
∴实数m的取值范围是[8-5ln 2,+∞).

练习册系列答案
相关题目

