题目内容
已知椭圆 =1(a>b>0)长轴长与短轴长之差是
=1(a>b>0)长轴长与短轴长之差是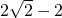 ,且右焦点F到此椭圆一个短轴端点的距离为
,且右焦点F到此椭圆一个短轴端点的距离为 ,点C(m,0)是线段OF上的一个动点(O为坐标原点).
,点C(m,0)是线段OF上的一个动点(O为坐标原点).
(I)求椭圆的方程;
(Ⅱ)是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得( +
+ )
) ,并说明理由.
,并说明理由.
解:(Ⅰ)由题意可知a-b= -1,又
-1,又 ,a2=b2+c2,
,a2=b2+c2,
解得a= ,b=c=1,
,b=c=1,
所以椭圆的方程为: ;
;
(Ⅱ)由(1)得F(1,0),所以0≤m≤1,
假设存在满足题意的直线l,设l的方程为y=k(x-1),代入 ,得(2k2+1)x2-4k2x+2k2-2=0,
,得(2k2+1)x2-4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),则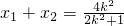 ,
,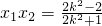 ①,y1+y2=k(x1+x2-2)=
①,y1+y2=k(x1+x2-2)= ,
,
所以 =(x1-m,y1)+(x2-m,y2)=(
=(x1-m,y1)+(x2-m,y2)=(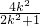 -2m,
-2m, ),
),
因为( +
+ )
) ,而AB的方向向量为(1,k),
,而AB的方向向量为(1,k),
所以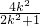 -2m+
-2m+ ×k=0?(1-2m)k2=m,
×k=0?(1-2m)k2=m,
所以当0≤m 时,k=±
时,k=± ,即存在这样的直线l;
,即存在这样的直线l;
当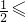 k≤1时,不存在这样的直线l.
k≤1时,不存在这样的直线l.
分析:(I)由长轴长与短轴长之差为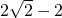 ,得2a-2b=
,得2a-2b=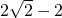 ,由右焦点F到此椭圆一个短轴端点的距离为
,由右焦点F到此椭圆一个短轴端点的距离为 ,可得a值;
,可得a值;
(Ⅱ)先由(1)求得m的范围,假设存在满足题意的直线l,设l的方程为y=k(x-1),A(x1,y1),B(x2,y2),由( +
+ )
) ,得(
,得( +
+ )•
)• =0①,易知AB的方向向量为(1,k),联立直线方程与椭圆方程构成方程组,消掉y得x的二次方程,由韦达定理、向量运算可用k表示
=0①,易知AB的方向向量为(1,k),联立直线方程与椭圆方程构成方程组,消掉y得x的二次方程,由韦达定理、向量运算可用k表示 +
+ ,代入①式得k的方程,有解则存在,否则即不存在;
,代入①式得k的方程,有解则存在,否则即不存在;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生的探究能力,考查学生对问题的分析解决能力,存在性问题常假设存在然后由此出发进行推理.
 -1,又
-1,又 ,a2=b2+c2,
,a2=b2+c2,解得a=
 ,b=c=1,
,b=c=1,所以椭圆的方程为:
 ;
;(Ⅱ)由(1)得F(1,0),所以0≤m≤1,
假设存在满足题意的直线l,设l的方程为y=k(x-1),代入
 ,得(2k2+1)x2-4k2x+2k2-2=0,
,得(2k2+1)x2-4k2x+2k2-2=0,设A(x1,y1),B(x2,y2),则
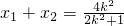 ,
,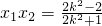 ①,y1+y2=k(x1+x2-2)=
①,y1+y2=k(x1+x2-2)= ,
,所以
 =(x1-m,y1)+(x2-m,y2)=(
=(x1-m,y1)+(x2-m,y2)=(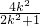 -2m,
-2m, ),
),因为(
 +
+ )
) ,而AB的方向向量为(1,k),
,而AB的方向向量为(1,k),所以
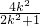 -2m+
-2m+ ×k=0?(1-2m)k2=m,
×k=0?(1-2m)k2=m,所以当0≤m
 时,k=±
时,k=± ,即存在这样的直线l;
,即存在这样的直线l;当
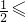 k≤1时,不存在这样的直线l.
k≤1时,不存在这样的直线l.分析:(I)由长轴长与短轴长之差为
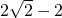 ,得2a-2b=
,得2a-2b=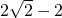 ,由右焦点F到此椭圆一个短轴端点的距离为
,由右焦点F到此椭圆一个短轴端点的距离为 ,可得a值;
,可得a值;(Ⅱ)先由(1)求得m的范围,假设存在满足题意的直线l,设l的方程为y=k(x-1),A(x1,y1),B(x2,y2),由(
 +
+ )
) ,得(
,得( +
+ )•
)• =0①,易知AB的方向向量为(1,k),联立直线方程与椭圆方程构成方程组,消掉y得x的二次方程,由韦达定理、向量运算可用k表示
=0①,易知AB的方向向量为(1,k),联立直线方程与椭圆方程构成方程组,消掉y得x的二次方程,由韦达定理、向量运算可用k表示 +
+ ,代入①式得k的方程,有解则存在,否则即不存在;
,代入①式得k的方程,有解则存在,否则即不存在;点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查学生的探究能力,考查学生对问题的分析解决能力,存在性问题常假设存在然后由此出发进行推理.

练习册系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)过点(1,
=1(a>b>0)过点(1, ),离心率为
),离心率为 =2;
=2; =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、