题目内容

在区间[-1，1]上随机的取两个数a，b，使得方程bx2+2ax+1=0有两个实根的概率为
2
3
2
3
．
分析：由题意可得，
-1≤a≤1
-1≤b≤1
为边长为2的正方形，面积为4，由方程bx2+2ax+1=0有两个实根a2≥b，根据积分知识可求其面积，代入概率求解公式可求
解答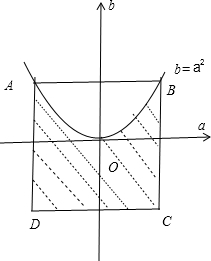：解：由题意可得，
-1≤a≤1
-1≤b≤1
，其区域为边长为2的正方形，面积为4
∵方程bx2+2ax+1=0有两个实根
∴△=4a2-4b≥0即a2≥b，其区域如图所示的阴影部分
其面积为S=2+
∫
1
-1
a2da=
1
3
a3
 
1
-1
+2=
8
3

概率P=
8
3
4
=
2
3

故答案为：
2
3
点评：本题主要考察了与面积有关的几何概率的求解，解题的关键是根据积分知识求解出基本事件的区域面积
练习册系列答案
相关题目
已知定义在区间[-1，1]上的函数为奇函数．．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
（3）f（x）在x∈[m，n]上的值域为[m，n]（-1≤m＜n≤1 ），求m+n的值．
已知定义在区间[-1，1]上的函数为奇函数．．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
（3）f（x）在x∈[m，n]上的值域为[m，n]（-1≤m＜n≤1 ），求m+n的值．
已知定义在区间[-1，1]上的函数为奇函数．．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
（3）f（x）在x∈[m，n]上的值域为[m，n]（-1≤m＜n≤1 ），求m+n的值．
已知定义在区间[-1，1]上的函数为奇函数．．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
（3）f（x）在x∈[m，n]上的值域为[m，n]（-1≤m＜n≤1 ），求m+n的值．
已知定义在区间[-1，1]上的函数为奇函数．．
（1）求实数b的值．
（2）判断函数f（x）在区间（-1，1）上的单调性，并证明你的结论．
（3）f（x）在x∈[m，n]上的值域为[m，n]（-1≤m＜n≤1 ），求m+n的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网