题目内容
已知函数f(x)=ln(x+a)-x2-x在x=0处取得极值。
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)若关于x的方程f(x)=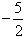 x+b在区间(0,2)有两个不等实根,求实数b的取值范围。
x+b在区间(0,2)有两个不等实根,求实数b的取值范围。
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)若关于x的方程f(x)=
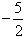 x+b在区间(0,2)有两个不等实根,求实数b的取值范围。
x+b在区间(0,2)有两个不等实根,求实数b的取值范围。解:(1)由已知得
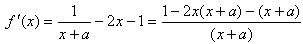
∵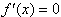
∴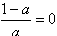
∴a=1。
(2)由(1)得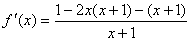
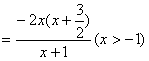
由
由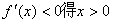
∴f(x)的单调递增区间为(-1,0),单调递减区间为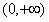 。
。
(3)令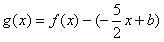
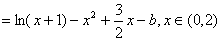
则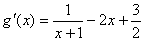
令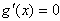 得
得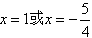 (舍)
(舍)
当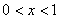 时,
时,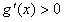
当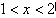 时,
时,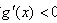 即
即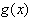 在
在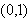 上递增,在(1,2)上递减
上递增,在(1,2)上递减
方程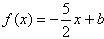 在区间
在区间 有两个不等实根
有两个不等实根
等价于函数g(x)在(0,2)上有两个不同的零点
∴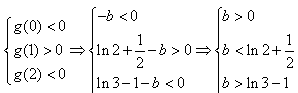
∴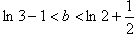
即实数b的取值范围为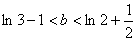 。
。
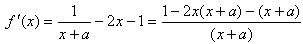
∵
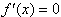
∴
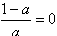
∴a=1。
(2)由(1)得
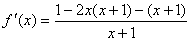
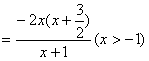
由

由
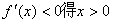
∴f(x)的单调递增区间为(-1,0),单调递减区间为
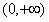 。
。(3)令
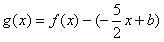
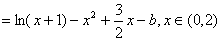
则
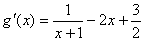
令
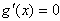 得
得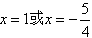 (舍)
(舍)当
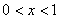 时,
时,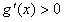
当
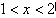 时,
时,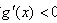 即
即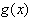 在
在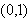 上递增,在(1,2)上递减
上递增,在(1,2)上递减 方程
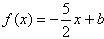 在区间
在区间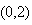 有两个不等实根
有两个不等实根等价于函数g(x)在(0,2)上有两个不同的零点
∴
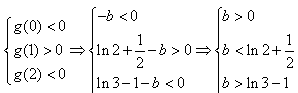
∴
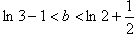
即实数b的取值范围为
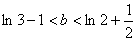 。
。
练习册系列答案
相关题目